Лекции ПБ 1.11

Readln

Begin

Begin

Uses

Begin

Begin

Begin

Var

Begin

Var

Begin

Var

Begin

Var

Const

Uses

Begin

Var

Begin

Var

Uses

Readln

Begin

Var

Uses

Readln

End

Begin

Else

Begin

Var

Uses

Readln

Begin

Var

Uses

Примеры программ

Учебно-практическое пособие

Правоведение

Часть 2

Подписано к печати:

Тираж:

Заказ №

Пример 1. Линейная программа.

{$APPTYPE CONSOLE}

SysUtils;

a,b,x1,x2,x3,x5,x6:Integer;x4:Real;

Readln(a,b);

X1:=a+b;

X2:=a-b;

X3:=a*b;

X4:=a/b;

X5:=a div b;

X6:=a mod b;

Writeln(' x1 = ',x1,' x2 = ',x2,' x3 = ',x3);

Writeln(' x4 = ',x4:12:6);

Writeln(' x5 = ',x5,' x6 = ',x6);

end.

Данная программа демонстрирует выполнение арифметических операций над целочисленными операндами.

В этой программе единственная переменная x4 имеет вещественный тип, так как частное от "обычного" деления целого числа на целое всегда имеет вещественный тип.

В конце программы стоит вызов процедуры Readln, которая приостанавливает выполнение программы до нажатия клавиши [Enter]. Это сделано для того, чтобы дать возможность просмотреть результаты программы до ее завершения. Аналогично с этой же целью такой же процедурой будут заканчиваться и программы, приведенные в остальных примерах.

Пример 2. Решение квадратных уравнений.

Составить программу для вычисления корней квадратного уравнения:

.

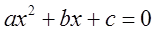Решение:

{$APPTYPE CONSOLE}

SysUtils;

a,b,c,x1,x2:Real;

err:Boolean;

procedure QuadroRoots(a,b,c:Real;var x1,x2:Real;

var err:Boolean);

var d:real;

err:=True;d:=b*b-4*a*c;

if d<0

then err:=False

x1:=(-b-Sqrt(d))/2/a;x2:=-b/a-x1

end;

begin {Начало головной программы}

Readln(a,b,c);

QuadroRoots(a,b,c,x1,x2,err);

if err

then Writeln(' x1 = ',x1:12:6,' x2 = ',x2:12:6)

else Writeln(' This equation has no roots');

end.

Квадратное уравнение, как известно, полностью определяется своими коэффициентами a, b и c, которые и являются исходными данными. Основные вычисления оформлены в виде процедуры с тремя входными (a, b и c) и тремя выходными (x1, x2 и err) параметрами. Параметр err имеет булевский тип; если его значение равно True, то уравнение имеет действительные корни, которые и выводятся на экран. В противном случае программа выводит на экран только сообщение о том, что уравнение не имеет действительных корней.

Пример 3. Вычисление значений функции на отрезке (табулирование функции).

Задана функция:

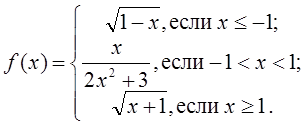
Составить программу для вычисления значений функции f (x) на отрезке [-3;4] с шагом D x =0,3.

Решение:

{$APPTYPE CONSOLE}

SysUtils;

a,b,dx,x,y:Real;

begin {Начало головной программы}

Readln(a,b,dx);

x:=a;

while x<=b do

if x<=-1 then y:=Sqrt(1-x);

if Abs(x)<1 then y:=x/(2*x*x+3);

if x>=1 then y:=Sqrt(x+1);

Writeln(' x = ',x:12:6,' f(x) = ',y:12:6);

x:=x+dx

end;

end.

Табулирование функции непосредственно реализовано с помощью оператора цикла с предусловием. Функция, как видно из постановки задачи, задана тремя ветвями: на интервале от –¥ до –1 она принимает значения выражения 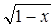; на интервале [–1;1] – значения выражения ; и, наконец, на интервале от 1 до +¥ – значения выражения 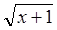. Вычисление значений функции во всех трех ветвях реализовано с использованием трех условных операторов IF в сокращенной форме IF...THEN.... Вычисление значений аргумента осуществляется так. Сначала задается его начальное значение (x:=a), затем в конце цикла значение x каждый раз изменяется, увеличиваясь на шаг dx. Вычисленные аргумент x и значение функции y выводятся на экран.

Пример 4. Вычисление суммы последовательности чисел, заданных общей формулой.

Составить программу для вычисления суммы:

Решение:

{$APPTYPE CONSOLE}

SysUtils;

Const N=17;

i:Integer;

s:Real;

s:=0;

for i:=1 to N do s:=s+(2*i+1)/(i*i+2);

Writeln(' s = ',s:13:7);

Readln

end.

Сумма чисел, заданных общей формулой, вычисляется в цикле путем накопление результата в переменой s. Перед тем, как реализовать цикл, задается начальное значение суммы, равное нулю.

Пример 5 (вариант предыдущего примера). Вычисление суммы элементов массива.

Задан одномерный массив действительных чисел a_k, k = 1,2, …, 20. Составить программу для вычисления суммы

.

Решение:

{$APPTYPE CONSOLE}

uses SysUtils;

Const N=20;

k:Integer;s:Real;

a: array [1..N] of Real;

for k:=1 to N do Read(a[k]);Readln;

s:=0; for k:=1 to N do s:=s+a[k];

Writeln(' s = ',s:13:7);

Readln

end.

Массив описан в разделе VAR. Элементы массива вводятся с помощью клавиатуры в одной строке, отделяются друг от друга пробелами. В конце ввода следует нажать [Enter]. Сумма вычисляется с помощью оператора цикла с параметром; ее начальное значение, равное нулю, задается до выполнения цикла, затем в цикле, как и в предыдущем примере производится ее накопление.

Пример 6. Вычисление среднего геометрического положительных элементов одномерного массива.

Задан одномерный массив a_k, k = 1,2, …, 25. Вычислить

.

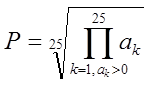Решение:

{$APPTYPE CONSOLE}

SysUtils;

N=25;

k,m:Integer;

p:Real;

a: array [1..N] of Real;

for k:=1 to N do Read(a[k]);Readln;

p:=1;m:=0;

for k:=1 to N do

if a[k]>0 then

begin p:=p+a[k];m:=m+1; end;

if m<>0 then Writeln(' p = ',Exp(Ln(p)/m):13:7)

else Writeln('No solve');

Readln

end.

Известно, что среднее геометрическое равно корню степени m из произведения заданных чисел, где m – количество этих чисел. Параметр m вначале задан равным нулю (в предположении, что положительных элементов в массиве может не быть). В программе выполняется проверка на положительность очередного элемента: если текущий элемент больше нуля, то, во-первых, выполняется умножение и, во-вторых, увеличение величины m на единицу (так как увеличилось на единицу число положительных элементов массива). Но, поскольку положительных элементов в массиве может не оказаться вообще, после завершения оператора цикла параметр m останется, равным нулю. В данном случае задача решений не имеет, что и должна вывести программа. Если же окажется, что этот параметр отличен от нуля, то задача имеет решение. Так как операция "возведение в степень" в языке Object Pascal отсутствует, ее придется заменить на некоторое выражение (в каждом конкретном случае – свое), связывающее экспоненту и логарифм (по определению логарифма ), что и реализовано в программе.

Пример 7. Нахождение наименьшего (наибольшего) элемента в массиве.

Задан одномерный массив a_k, k = 1,2, …, 15. Найти

.

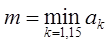Решение:

{$APPTYPE CONSOLE}

uses SysUtils;

Const N=15;

k:Integer;min:Real;

a: array [1..N] of Real;

for k:=1 to N do Read(a[k]);Readln;

min:=a[1];

for k:=2 to N do

if a[k]<min then min:=a[k];

Writeln(' min = ',min:10:4);Readln

end.

В данной программе реализован так называемый метод "пузырька". Сначала предполагается, что наименьшим элементом является первый элемент в массиве. Затем в цикле выполняется проверка. Если очередной элемент меньше текущего минимального, то последнему присваивается значение этого элемента, в противном случае ничего не выполняется.

Пример 8 (вариант предыдущего примера). Задан одномерный массив a_k, k = 1,2, …, 15. Найти наибольший положительный элемент массива и его номер.

Решение:

{$APPTYPE CONSOLE}

uses SysUtils;

Const N=15;

k,m:Integer;max:Real;

a: array [1..N] of Real;

for k:=1 to N do Read(a[k]);

Readln;

max:=0; m:=0;

for k:=1 to N do

if a[k]>max then begin max:=a[k];m:=k; end;

if m>0

then Writeln(' a[',m:1,'] = ',max:10:4)

else Writeln(' No solve');

Readln

end.

Задача решается аналогично предыдущей. Отличие лишь в том, что, во-первых, выполняется поиск наибольшего значения (поэтому в программе знак "<" заменен на ">") и, во-вторых, выполняется поиск наибольшего из положительных элементов массива (поэтому в программе выполняется проверка на положительность). Данная задача может не иметь решения, если все элементы массива отрицательные. Поэтому при m>0 выводится наибольший элемент с его номером; в противном случае – сообщение о том, что решений нет.

Пример 9. Преобразование массива.

Задан одномерный массив из 18 вещественных чисел. Получить новый массив, в котором все положительные элементы исходного массива заменены нулями.

Решение:

{$APPTYPE CONSOLE}

uses SysUtils;

Const N=18;

k,i:Integer;a,b: array [1..N] of Real;

for k:=1 to N do Read(a[k]);Readln;

for k:=1 to N do

if a[k]>0 then b[k]:=0 else b[k]:=a[k];

Writeln(' a = ',a[k]:10:4,' b = ',b[k]:10:4);

end;

Readln

end.

Программа выводит на экран два массива (в виде двух столбцов).

Пример 10. Рекуррентное преобразование массива.

Задана последовательность чисел, называемых числами Фибоначчи, определяемых следующими соотношениями:

F ₀ = 1; F ₁ = 1; …; F_k = F_{k -1} + F_{k -2}, k = 2,3,…, N,…

Вычислить первые не более 1001 (то есть до N =1000) чисел Фибоначчи.

Решение:

Uses SysUtils;

Const NN=1000;

label 1;

var N,k:Integer;F: array [0..NN] of Real;

Readln(N);

F[0]:=1; if N=0 then goto 1;

F[1]:=1; if N=1 then goto 1;

for k:=2 to N do F[k]:=F[k-1]+F[k-2];

1: for k:=0 to N do Writeln(' F[',k:3,'] = ',F[k]);

Readln

end.

Первые два числа Фибоначчи задаются, равными 1, остальные вычисляются в цикле. Программа рассчитана только до N=1000 (в противном случае произойдет ошибка при проверке границ массива).

Пример 11. Вычисление корней нелинейного уравнения.

Составить программу для решения нелинейного уравнения:

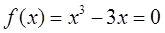
итерационным методом дихотомии (половинного деления отрезка) с заданной точностью e>0.

Решение:

{$APPTYPE CONSOLE}

SysUtils;

label 1,2,3;

var a,b,x,y,eps:Real;

function f(x:Real):Real;

f:=x*x*x-3*x

end;

Readln(eps);

1:Readln(a,b);

if f(a)*f(b)>0

then begin Write(Input a and b: '); goto 1; end;

2:x:=(a+b)/2;

if Abs(f(x))<eps then goto 3;

if f(a)*f(x)<0 then b:=x else a:=x;

goto 2;

3:Writeln(' f(',x:12:6,') = ',f(x):13:7);

end.

В данной программе реализовано два цикла. Оба цикла организуются операторами IF и GOTO. Такие циклы принято называть неявными. Вычисление функции f (x) оформлено в виде нестандартной функции. На первом этапе вводится точность e>0 (близкое к нулю положительное число) и концы интервала (a, b), на котором ищется корень, и происходит проверка, существует ли на этом интервале хотя бы один корень. Если нет, то концы интервала вводятся заново. Если да, то процесс продолжается. С этой целью находится середина интервала (a, b) и следом проверяется, достигнута ли требуемая точность. Если да, то результат считается найденным и выводится на экран; в противном случае проверяется, в какой из половин интервала (левой или правой) находится корень и соответствующим образом меняются концы интервала. Затем находится середина нового интервала. И так далее. Таким образом, интервал (a, b) с каждым шагом сужается. Рано или поздно, корень будет найден, как только требуемая точность будет достигнута.

В некоторых случаях может произойти "зависание" или "зацикливание" программы, если текущее значение x оказывается равным его предыдущему. Для того, чтобы программа всегда завершалась сама, вводится ограничитель числа итераций (скажем, ограничить число повторений последнего неявного цикла до 100 или 1000). Если программа завершилась по истечению заданного числа итераций, то требуемая точность может быть еще не достигнута. Тогда применяются другие приемы. Например, можно уменьшить точность или увеличить ограничитель числа итераций, изменить концы интервала, на котором находится корень. С целью уточнения концов интервала, можно предварительно вывести таблицу значений функции на выбранном интервале, а затем ввести другие концы интервала, а именно, где функция меняет знак.

Дата добавления: 2014-01-07