
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Отражение и преломление плоской волны на границе
|
|
|
|
раздела двух диэлектриков.
Рассмотрим падение плоской электромагнитной волны на плоскую границу раздела двух диэлектриков.
Плоскостью падения волны называется плоскость, перпендикулярная границе раздела сред и содержащая волновой вектор падающей волны.
Будем предполагать, что волна является линейно-поляризованной. Уравнения волны  ,
,  ,
, 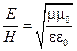 .
.
Ход каждой из волн зададим с помощью лучей и соответствующих волновых векторов.
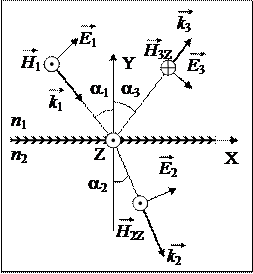 Рассмотрим любую точку на границе. В ней пересекаются три луча – луч падающей волны, луч прошедшей волны и луч отражённой волны.
Рассмотрим любую точку на границе. В ней пересекаются три луча – луч падающей волны, луч прошедшей волны и луч отражённой волны.
Вдоль границы введём систему координат так, чтобы волновой вектор падающей волны лежал в плоскости (XY), где ось X направлена вдоль границы, а вектор Y перпендикулярен ей, а начало координат совпадало с выбранной точкой.
Тогда  , где угол a 1 между нормалью к границе (осью Y) и лучом падающей волны будем называть углом падения.
, где угол a 1 между нормалью к границе (осью Y) и лучом падающей волны будем называть углом падения.
Будем обозначать параметры падающей волны индексом «1», прошедшей волны - индексом «2», а отражённой – «3». Введём угол преломления a2 и угол отражения a3 - углы между нормалью и соответствующими лучами. Тогда
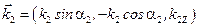 ,
, 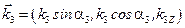 .
.
В общем случае падающую волну можно представить в виде суперпозиции двух волн, у которых плоскости поляризации взаимно перпендикулярны. Поэтому рассмотрим падение волн с такой поляризацией по-отдельности.
1) Рассмотрим случай, когда в падающей волне вектор  параллелен границе, а вектор
параллелен границе, а вектор 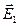 лежит в плоскости (XY), т.е.
лежит в плоскости (XY), т.е.  . Как говорят, волна поляризована в плоскости падения.
. Как говорят, волна поляризована в плоскости падения.
Так как на границе должны выполняться условия 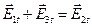 и
и  , то
, то 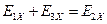 и
и 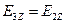 ,
, 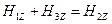 и
и  .
.
Кроме того, на границе выполняются условия  и
и 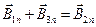 ,
,
поэтому 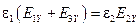 ,
,  .
.
Как следует из этих уравнений проекции E 2Z, E 3Z, H 2X, H 3X, H 2Y, H 3Y не связаны никакими уравнениями с параметрами падающей волны. Поэтому их можно не рассматривать, т.е. считать равными нулю. Следовательно, прошедшая и отражённая волны являются линейно-поляризованными, т.к.
 ,
, 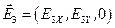 ,
, 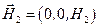 ,
, 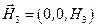 .
.
Тогда волновые векторы тоже лежат в плоскости (XY):
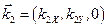 ,
,  .
.
Уравнения для напряжённостей всех трех волн
 ,
,  ,
,  .
.
Для них должно выполняться условие на границе 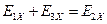 . Точки границы задаются радиус-вектором
. Точки границы задаются радиус-вектором 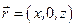 , поэтому на границе выполняется равенство:
, поэтому на границе выполняется равенство:
 .
.
В частности, в точке x =0: 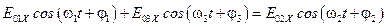 .
.
 На амплитудно-векторной диаграмме сумма трёх векторов постоянной длины
На амплитудно-векторной диаграмме сумма трёх векторов постоянной длины 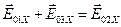 не будет зависеть от времени, если только угловые скорости вращения этих векторов одинаковые:
не будет зависеть от времени, если только угловые скорости вращения этих векторов одинаковые:  . Т.е. частоты всех трёх волн одинаковые. Обозначим эту частоту w.
. Т.е. частоты всех трёх волн одинаковые. Обозначим эту частоту w.
Теперь зафиксируем какой-то момент времени t 0. Тогда в любой точке границы (для любого значения x) выполняется равенство:
 .
.
Так как величина x является параметром, то волновые числа k 1 X, k 2 X, k 3 X будут являться аналогом угловой скорости вращения векторов 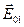 ,
,  ,
, 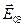 на амплитудно-векторной диаграмме. Следовательно, равенство
на амплитудно-векторной диаграмме. Следовательно, равенство 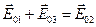 возможно только в случае, когда k 1 X = k 2 X = k 3 X.
возможно только в случае, когда k 1 X = k 2 X = k 3 X.
Из k 1 X = k 2 X следует соотношение  . Т.к.
. Т.к.  и
и 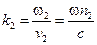 , то угол падения и угол преломления связаны соотношением:
, то угол падения и угол преломления связаны соотношением:

(закон Снеллиуса).
 Из k 1 X = k 3 X следует соотношение
Из k 1 X = k 3 X следует соотношение 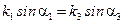 . Т.к. падающая и отражённая волны распространяются в одной среде, то
. Т.к. падающая и отражённая волны распространяются в одной среде, то 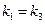 , откуда
, откуда  - угол отражения равен углу падения.
- угол отражения равен углу падения.
Найдём соотношения между величинами напряжённостей. Предположим, что векторы напряжённостей электрического и магнитного полей в падающей, прошедшей и отражённой волнах в некоторый момент времени имеют направления, указанные на рисунке. Тогда  ,
, 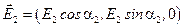 и
и  .
.
Условие 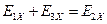 примет вид:
примет вид:
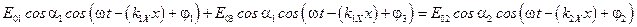 .
.
Из условия: 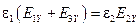 получаем равенство:
получаем равенство:
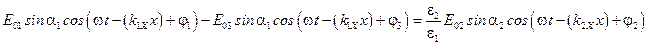
Получаем систему из двух уравнений
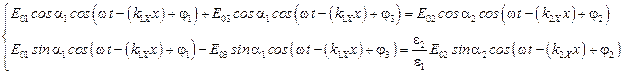 .
.
Из закона преломления  следует, что уравнения выполняются в случае нормального падения волны на границу
следует, что уравнения выполняются в случае нормального падения волны на границу 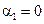 .
.
Предположим, что  . Первое уравнение умножаем на
. Первое уравнение умножаем на 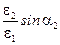 , а второе на
, а второе на  и, вычитая из первого уравнения второе, получаем:
и, вычитая из первого уравнения второе, получаем:
 .
.
Преобразуем это уравнение
 В этом уравнении коэффициенты при
В этом уравнении коэффициенты при 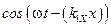 и
и 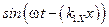 не зависят от времени. Поэтому они должны быть равными нулю. Равенства
не зависят от времени. Поэтому они должны быть равными нулю. Равенства
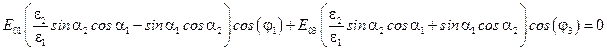 , и
, и

выполняются одновременно при  и
и  .
.
Перепишем эти условия в виде 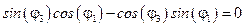 и получим, что
и получим, что
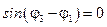 , т.е. начальные фазы падающей и отражённой волн либо равны, либо отличаются друг от друга на p. Поэтому
, т.е. начальные фазы падающей и отражённой волн либо равны, либо отличаются друг от друга на p. Поэтому  (либо
(либо 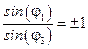 ). Тогда можно записать:
). Тогда можно записать:
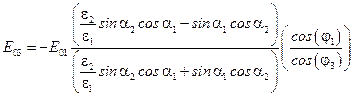 .
.
Для оптически прозрачных сред 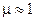 , поэтому
, поэтому  . С учётом
. С учётом  ,
, 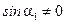 можно провести некоторые преобразования и получить
можно провести некоторые преобразования и получить
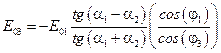 .
.
Величины амплитуд Е 01 и Е 03 положительные.
Т.к. a1 £ p/2 и a2 £ p/2, то a1+a2 £ p, поэтому tg (a1+a2) ³ 0.
Следовательно, в случае a1-a2 ³ 0, (т.е. когда tg (a1-a2) ³ 0) должно быть
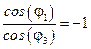 - фаза отражённой волны отличается от фазы падающей волны на p.
- фаза отражённой волны отличается от фазы падающей волны на p.
В этом случае a1 ³ a2, поэтому 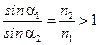 , т.е. волна отражается от оптически более плотной среды.
, т.е. волна отражается от оптически более плотной среды.
Случаю a1-a2 < 0 соответствует отражение от оптически менее плотной среды и фаза отражённой волны совпадает с фазой падающей волны.
Возможен случай, когда нет отражённой волны: Е 03= 0. Это возможно либо при tg (a1-a2)=0, т.е. a1=a2 - волна не преломляется, либо при tg (a1+a2)→ +¥, т.е. a1+a2 =p/2 - волновые векторы преломлённого луча и отражённого луча взаимно перпендикулярны.
Тогда равенство Е 03=0 равносильно 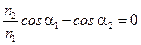 . Но
. Но 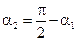 , поэтому
, поэтому  . Следовательно, если тангенс угла падения равен относительному показателю преломления двух сред,
. Следовательно, если тангенс угла падения равен относительному показателю преломления двух сред,

то при отражении света от границы между ними нет волны, плоскость поляризации которой совпадает с плоскостью падения. Этот угол называется углом Брюстера.
Дальнейшее решение приводит к выражению:
 .
.
Величины амплитуд Е 01 и Е 02 положительные.
Т.к. a1£p/2 и a2£p/2, то a1+a2£p, поэтому sin (a1+a2)³0 и cos (a2-a1)³0. Следовательно, должно быть 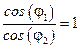 , т.е. фазы прошедшей и падающей волн совпадают.
, т.е. фазы прошедшей и падающей волн совпадают.
2) Рассмотрим случай, когда в падающей волне вектор 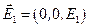 параллелен границе, а вектор
параллелен границе, а вектор  лежит в плоскости (XY), т.е.
лежит в плоскости (XY), т.е. 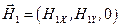 . Волна поляризована в плоскости, перпендикулярной плоскости падения.
. Волна поляризована в плоскости, перпендикулярной плоскости падения.
Так как на границе должны выполняться условия 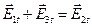 и
и 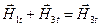 , то
, то
 и
и 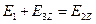 ,
, 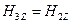 и
и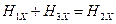 .
.
Кроме того, на границе выполняются условия  и
и 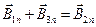 ,
,
поэтому 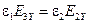 ,
, 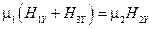 .
.
Координаты E 2X, E 3X, E 2Y, E 3Y, H 2Z, H 3Z, не связаны никакими уравнениями с параметрами падающей волны. Поэтому их можно не рассматривать, т.е. считать равными нулю. Следовательно, прошедшая и отражённая волны являются линейно-поляризованными, т.к.
 ,
,  ,
, 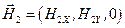 ,
, 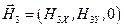 .
.
Результаты решения для этого случая сформулируем следующим образом.
Законы преломления остаются прежними 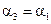 ,
,  .
.

Т.к. a1£p/2 и a2£p/2, то a1+a2£p, поэтому tg (a1+a2)³0.
Следовательно, в случае a1-a2³0, (т.е. когда sin (a1-a2)³0) должно быть
 - фаза отражённой волны отличается от фазы падающей волны на p.
- фаза отражённой волны отличается от фазы падающей волны на p.
В этом случае a1³a2, поэтому 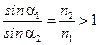 , т.е. волна отражается от оптически более плотной среды.
, т.е. волна отражается от оптически более плотной среды.
Случаю a1-a2<0 соответствует отражение от оптически менее плотной среды и фаза отражённой волны совпадает с фазой падающей волны.

Поэтому должно быть 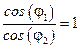 , т.е. фазы преломлённой и падающей волн одинаковые.
, т.е. фазы преломлённой и падающей волн одинаковые.
В итоге, закон преломления можно сформулировать следующим образом. Волновые векторы всех трёх волн лежат в одной плоскости падения. Угол падения равен углу отражения, угол преломления связан с углом отражения соотношением
 .
.
Фазы падающей и прошедшей волн одинаковые. Фаза отраженной волны отличается от фазы падающей волны на p при отражении от оптически более плотной среды.
Падающая волна, отражённая и преломлённая волны поляризованы одинаково. Но если волна, поляризованная в плоскости падения, падает под углом Брюстера  , то отраженная волна отсутствует.
, то отраженная волна отсутствует.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 743; Нарушение авторских прав?; Мы поможем в написании вашей работы!