Проводимость металлов

В периодическом поле кристалла появляются ограничения на значения энергии в виде разрешённых и запрещённых зон. Поэтому зависимость между энергией и волновым числом будет существовать только на определённых интервалах волновых чисел. Эти интервалы называются зонами Бриллюэна.

1-я зона Бриллюэна соответствует интервалу: 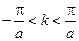, 2-я зона - объединению интервалов: 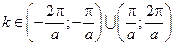и т.д.

Внутри конечного кристалла размером L могут двигаться свободно только частицы в состояниях, для которых длина волны де Бройля целочисленно кратна размеру ячейки: 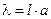, или, с учётом размера ячейки , где N – число ячеек, получаем, что 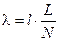. Откуда для волнового числа следует равенство: 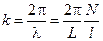. Т.к. 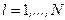, то в пределах одной разрешённой энергетической зоны существует N дискретных значений энергии. Поэтому расстояние между этими дискретными уровнями энергии в пределах одной зоны, обратно

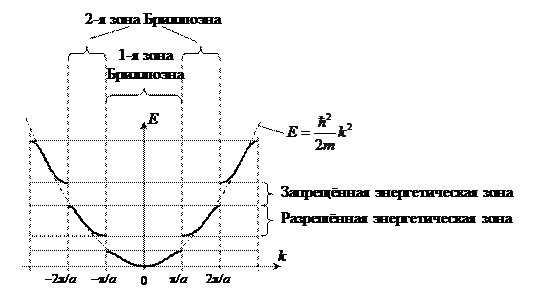пропорционально числу ячеек в кристалле. Т.е. уровни энергии расположены настолько близко, что распределение энергии в пределах одной энергетической зоны можно считать квазинепрерывным.

При рассмотрении реальных трёхмерных кристаллов используют теорему Флюге-Блоха о виде пси-функции для решения уравнения Шрёдингера в трёхмерных кристаллах.

Пусть вектор 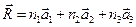- такой вектор, что наборы целых чисел 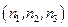определяют положения атомов в кристаллической решётке, тогда

,

откуда следует, что сдвиг аргумента волновой функции в направлении вектора 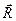аналогичен умножению функции на фазовый множитель 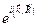, где 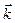- некоторый вектор.

Поэтому решение уравнения Шрёдингера:

в трёхмерных кристаллах следует искать в виде: , где функция 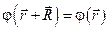, периодическая по кристаллу, называется функцией (или волной) Блоха.

При поиске решения возникают соотношения между разрешёнными зонами энергии Е и координатами вектора . Такие зависимости в трёхмерном пространстве также называют зонами Бриллюэна.

Зоны Бриллюэна - это области значений волнового вектора 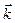, в которых энергия электронов изменяется непрерывно, а на границах претерпевает разрыв.

Понятие зоны Бриллюэна играет важнейшую роль в физике твёрдого тела. Например, установлено, что на кристаллической решётке дифрагируют только те лучи, волновой вектор которых оканчивается на границе зоны Бриллюэна.

Из-за периодичности кристаллической решётки и наличия зон Бриллюэна в кристалле возникают запрещённые и разрешённые энергетические состояния. Возникновение запрещённых зон связано с тем, что для волн (определённых длин волн де Бройля электрона) на границе зон Бриллюэна возникает условие брэгговского отражения, и волна отражается от границы зоны. Физически это равносильно тому, что возникает стоячая волна, и, следовательно, групповая скорость данной электронной волны равна нулю. Таким образом, возникает интервал запрещённых частот (т.е. энергий).

Рассмотрим движение электрона, участвующего в электропроводимости, с точки зрения классической физики. На электрон со стороны внешнего электрического поля действует сила 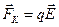, а со стороны усреднённого поля решётки металла и других электронов действует сила сопротивления 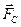, поэтому уравнение движения имеет вид: . Электрический ток создаётся упорядоченным движением заряженных частиц, движущихся с установившейся скоростью (скоростью дрейфа).

Если рассматривать волновое описание движения электронов, то как описать электропроводность в этом случае? Оказывается, что классическое рассмотрение и в этом случае остаётся справедливым, только необходимо модифицировать некоторые классические понятия.

Введём понятие эффективной массы электрона, движущегося в периодическом поле кристалла. Уравнение движения оставим в прежнем виде: 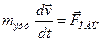. Предположим, что электрон движется вдоль силовой линии поля, поэтому вдоль линии тока можно перейти от векторов к скалярам: .

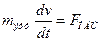В качестве скорости электрона примем групповую скорость волнового пакета: 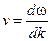. Т.к. 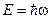, то 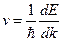. Найдем ускорение: 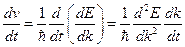. (Здесь использовано соотношение: .)

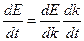Мощность силы равна скорости изменения кинетической энергии: 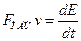. Тогда

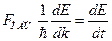или 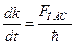. Подставим это выражение в формулу для ускорения:

или 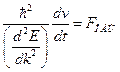. Поэтому эффективная масса электрона принимает вид:

.

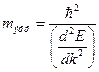Для свободно движущегося электрона 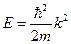, поэтому 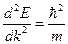и 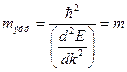, т.е. совпадает с обычной массой.

Если электрон движется в периодическом поле кристалла, то зависимость 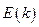непрерывна в пределах зон Бриллюэна.

Рассмотрим, например, вторую зону. Точка А находится на нижней границе зоны, поэтому под действием внешней силы скорость электронов должна только увеличиваться (на границе зоны функция 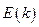терпит разрыв). Т.е. 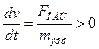, откуда 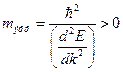, поэтому в этой точке 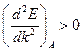. Соответственно, точка В находится на верхней границе зоны, поэтому под действием внешней силы скорость электронов должна только уменьшаться. Т.е. 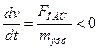, откуда 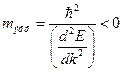, поэтому в этой точке 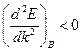. Тогда существует точка перегиба графика - точка С, в которой 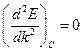. В этой точке 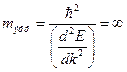, т.е электрон не «реагирует» на внешнюю силу - ускорение равно нулю: 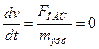. Соответствующую скорость можно принять за скорость дрейфа.

Замечание. В реальных кристаллах эффективная масса зависит от направления движения, т.е. является тензорной величиной.

Дата добавления: 2014-01-07