Теорема умножения вероятностей

Условная вероятность

Зависимые и независимые события.

Два события называются независимыми, если появление и не появление одного из них никак не влияет на вероятность другого события.

Пример: Одновременно брошены 2 игральных кубика. Пусть событие A - на первом кубике выпало 5 очков; событие B- на втором 6 очков. События A и B независимы, т.к. оба кубика бросаются независимо друг от друга.

Несколько событий называются попарно независимыми, если каждые два из них независимы.

Два события называются зависимыми, если вероятности осуществления одного из них зависит от появления или не появления другого события.

Пример: Пусть в урне находятся белые и черные шары.

а) Вероятность вынуть во второй раз белый шар из урны, если вынутый первым шар предварительно возвращен, не зависит от того, белый или черный шар был вынут в первый раз. Поэтому результаты первого и второго вынимания независимы между собой.

б)Наоборот, если шар, вынутый первым, не возвращается в урну, то результат второго вынимания зависит от первого, ибо состав шаров, находящихся в урне после первого вынимания, меняется в зависимости от его исхода. Это зависимые события.

Пусть A и B - зависимые события, из определения зависимых событий, что вероятность одного из событий зависит от появления или не появления другого события, важно знать наступило ли другое событие.

Условная вероятность события- вероятность, вычисляемая в предположении, что событие A уже наступило.

Вероятность совместного появления 2-х событий равна произведению вероятностей одного из них на словную вероятность другого, вычисленную в предположении, что 1-ое событие уже наступило.

Пусть n- число всех возможных исходов опыта, в котором событие A наступает или не наступает, m -число исходов, благоприятствующих событию A, l- число событий благоприятствующих A×B, в котором событие A уже наступило.

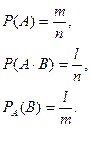
Считаем, что событие A уже наступило, то из раннее возможных n -случаев остаются возможными только те m -которые благоприятствуют событию A, из них l-исходв благоприятствуют событию B.

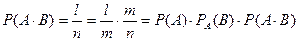
Замечание 1:

Для независимых событий условная вероятность совпадает с безусловной, поэтому вероятность от произведения равна произведению этих событий.

Замечание 2:

Теорема умножения обобщается на любое число сомножителей при условии, что эти события независимой совокупности.

Несколько событий называются независимыми в совокупности, если вероятность появления одного из них не зависит от того произошли ли какие- либо рассматриваемые события или нет.

Пример:

Студент пришел на экзамен зная 20 вопросов из 25 вопросов. Какова вероятность того, что студент знает каждый из 2-х вопросов, заданных ему экзаменатором?

Пусть событие A - студент знает 1-й вопрос.

B -студент знает 2-й вопрос, тогда вероятность события A,

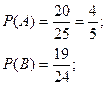искомая вероятность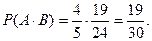

Дата добавления: 2014-01-07