Числовые характеристики случайных величин

Математическое ожидание случайной величины.

Закон распределения, как известно, полностью характеризует случайную величину.

Однако, отыскание закона распределения часто связано с большими трудностями. Но в ряде случаев, для решения практических важных задач, можно ограничиться рассмотрением лишь некоторых характеристик распределения.

Одной из самых важных характеристик распределения случайной величины являются ее математическое ожидание или среднее значение.

Определение 1. Рассмотрим дискретную случайную величину, имеющую следующее определение.

xi	x1	x2…..	xn
Pi	P1	P2…...	Pn

Математическим ожиданием дискретной случайной величины называется число M[x] равное сумме произведений всех ее возможных значений x_i на вероятности Pi.

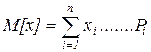
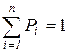
Если множество возможностей величины бесконечно, то конечную сумму этого ряда заменяют при условии, что ряд этот сходится, в противном случае это не производится.

Вероятностный смысл.

Пусть произведено N – независимых испытаний, в которых случайная величина приняла значение:

m раз – х_1;

m₂ раз – х_2;

……………;

m_n раз - х_n.

Определим среднее значение этой случайной величины x

m₁+m₂+…….+m_n=N, тогда среднее значение случайной величины составит:

;

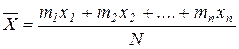
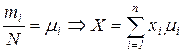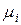-частота появления значения x_i.

При большом числе испытаний частота будет группироваться около соответствующих вероятностей.

N®¥Þm_i»Pi Þ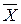»M[x]

Поэтому математическое ожидание называют средним значением случайной величины x (равенство тем точнее, чем больше число испытаний).

Механический смысл математического ожидания.

Математическое ожидание M[x] называют центром распределения случайной величины x. Это название будет аналогично с понятием центра тяжести материальных точек, расположенных на одной прямой, если на x в n точках с координатами x ₁, x ₂ …x_n, сосредоточены массы Р₁, Р₂…Рn, то координата центра тяжести x_c находится по формуле:

.

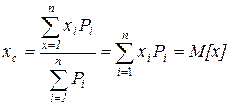Из определения математического ожидания следует, что математическое ожидание есть неслучайная (постоянная) величина.

Пример:

Вероятность изготовления нестандартного изделия при налаженном технологическом процессе равна 0,1. Для проверки качества изготавливаемых изделий ОТК берем из партии не более 4-х изделий. При обнаружении нестандартного изделия вся партия задерживается. Найти математическое ожидание (среднее значение) числа изделий, проверяемых ОТК из каждой из партии.

Решение:

x -число изделий, проверяемых ОТК в каждой партии.

Составим ряд распределения для x.

x
P	0,1	0,09	0,081	0,729

P (x =2)=0,9×0,1=0,09;

P (x =3)=0,9×0,9×0,1=0,081;

P (x =4)=0,9⁴+0,9³×0,1=0,9³(0,9+0,1)=0,729;

M [ x ]=1×0,1+2×0,09+3×0,081+4×0,729=3,439.

Математическое ожидание непрерывной случайной величины.

Пусть f(x) – плотность распределения непрерывной случайной величины.

Определение: Математическим ожиданием непрерывной случайной величины называется интеграл от ее значений x на плотность распределения f(x).

M[x]=.

f(e_i)

Несобственный интеграл предполагается абсолютно сходящимся, в противном случае говорят, что математического ожидания не существует.

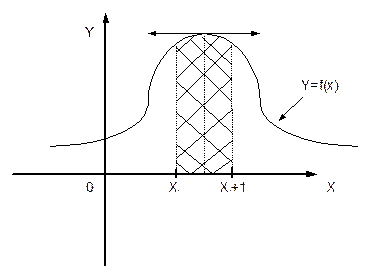Если функция f(x) симметрична относительно некоторой точки х=а, то математическое ожидание равно а. Математическое ожидание всегда имеет ту же размерность, что и значение случайной величины.

Дата добавления: 2014-01-07