Функция от случайных величин

Определение: Под функцией j(х) случайной величины Х понимают такую случайную величину у, которая принимает значения у=j(х) каждый раз, когда величина Х принимает значение х.

1. Пусть аргумент Х – дискретная случайная величина с возможными значениями х₁, х₂, х₃, …..х_n и вероятностями Р₁, Р₂, Р₃…..Р_n. Пусть для различных возможных значений x_i, значения функции j(х_i) также различны. Возможными значениями случайной величины случайной величины у будут значения функции j(х_i) тогда и только тогда, когда величина Х примет значение х_i, поэтому вероятности их равны, т.е.

Р(Y=j(х_i))=P(X=x_i)=P_i

Т.к. событие - величина X приняла значение x_i влечет за собой событие-величина у приняла значение у_i=j(х_i) и обратно эти события равносильны и следовательно равновероятностные.

Пример 1.

Случайная величина задана распределением

x	-2
Р	0,1	0,5	0,3	0,1

Найти закон распределения вероятностей величин х², 3х, х²+1.

у=х²

x^2
Р	0,1	0,5	0,3	0,1

у=3х

3x	-6
Р	0,1	0,5	0,3	0,1

у=х²+1

x^2+1
Р	0,1	0,5	0,3	0,1

Пример 2.

Дано распределение

x	-2
Р	0,4	0,5	0,1

Найти распределение величины у=х²

x
Р	0,4	0,5	0,1

Событие х²=4 есть сумма 2-х событий х=-2 и х=2, поэтому по правилу сложения вероятностей

Р(х²=4)=0,4+0,5=0,9

Тогда пишут

У
Р	0,9	0,1

Пример 3. даны две независимые случайные величины х и у.

Х	-1
Р	0,2	0,3	0,5

У
Р	0,1	0,3	0,6

Составить закон распределения величины z=(х×у)

N	x	y	x×y	P
	-1 -1 -1		0,02 0,06 0,12 0,03 0,09 0,18 0,05 0,15 0,3	-1 -3

Р (z =0)=0,03+0,09+0,18+0,05+0,02+0,02+0,08+0,27=0,37

z	-3	-1
Р	0,12	0,06	0,37	0,15	0,3

Т.к. случай z =0 – несовместимое событие, то по теореме сложения Р (0) складываем.

2) Пусть аргумент x непрерывная случайная величина. Как найти распределение функции у=j(х), зная плотность распределения f(x) аргумента x.

Рассмотрим монотонную функцию от одной случайной величины. Пусть в интервале возможных случайных значений х (a;b) функция строго возрастает, т.е. если х₂>х₁ то у₂>у₁.

Пусть аргумент x непрерывная случайная величина. Как найти распределение y=j(x), зная плотность распределения f(x) случайного аргумента x. Рассмотрим монотонную функцию от одной случайной величены. Пусть в интервале возможных значений от а до b функция строго возрастает.

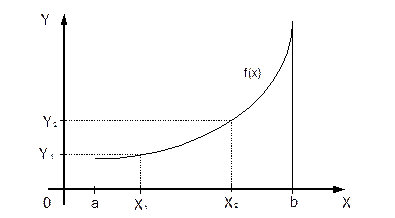Кроме того, функция непрерывна вместе со своей 1-ой производной и имеет непрерывную дифференцируемую функцию, каждый внутренний интервал от x ₁ до х ₂ взаимно однозначно отображается на соответствующем интервале от у ₁ до у ₂ потому: Р(у₁<у<у₂)=Р(х₁<x<x₂) вероятности попадания случайной величены х и у это есть двумерная величена.

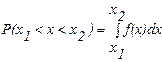-двумерная величина.

В этом интервале заменяем х на функцию g(y) обратную к функции y=j(x)

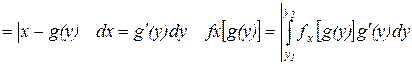
сравнивая с равенством (1) мы отмечаем, что подинтегральная функция – есть плотность распределения непрерывности случайной величены у.

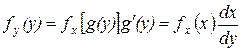в дифференцируемой форме .

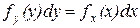Дата добавления: 2014-01-07