Теорема Чебышева

Основная форма закона больших чисел.

Рассмотрим последовательность попарно независимые случайные величины х₁,х₂…….х_n. Пусть все они имеют математическое ожидание и дисперсии. M[x₁], D[x₁] и средняя арифметическая из первых n -величин.

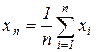
Распишем

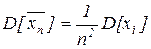. Пусть все дисперсии x_n ограничены числом с, 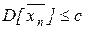, тогда . Отсюда видно, что дисперсия от среднего → 0 при n → ¥. Применяя к неравенство Чебышева:

или заменим .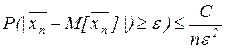

Правая часть неравенства ® 0, при n ® ¥, а левая неотрицательна, потому из данного неравенства следует что 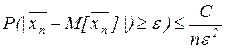, при n ® ¥

,

.

Таким образом, теорема Чебышева утверждает, что если рассматривается довольно большое число попарно независимых случайных величин имеющих ограниченные дисперсии, то почти достоверно можно считать, что средняя арифметическая случайной величины сходятся по вероятности со средней арифметической их математического ожидания.

Частный случай – все случайные величины имеют одно и тоже M[x], тогда

M[x]=a,

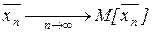, в частном случае

Дата добавления: 2014-01-07