Основные свойства преобразования Фурье

Между колебанием s(t) и его спектром S(w) существует однозначное соответствие. Для практических приложений важно установить связь между преобразованием колебания и соответствующим ему изменением спектра. Из многочисленных возможных преобразований колебания рассмотрим следующие наиболее важные и часто встречающиеся: сдвиг колебания во времени, изменение масштаба времени, сдвиг спектра колебания по частоте, дифференцирование и интегрирование колебания, сложение, произведение и свертка двух колебаний, а также свойства взаимной обратимости w и t в преобразованиях Фурье.

2.4.1 Сдвиг колебания во времени

Пусть колебание s₁(t) произвольной формы существует на интервале времени от t₁ до t₂ и обладает спектральной плотностью S₁(w), т.е. известен закон соответствия s₁(t) «S₁(w). Рассмотрим такой же сигнал, но возникающий на t₀ секунд позднее. Принимая точку t₀ за новое начало отсчета времени, получим новый смещенный сигнал s₂(t) = s₁(t - t₀). Тогда спектральная плотность смещенного колебания после введения новой переменной t = t - t₀ в соответствии с (2.24) определится как:

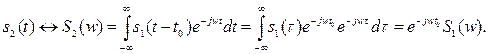(2.31)

Из этого соотношения видно, что сдвиг во времени функции s(t) на величину ±t₀ приводит к изменению фазовой характеристики спектра S(w) на величину ±wt₀. Очевидно и обратное положение: если всем составляющим спектра функции s(t) дать фазовый сдвиг j(w) = ±wt₀, линейно связанный с частотой w, то функция сдвигается во времени на величину ±t₀.

Амплитудно-частотная характеристика спектра (т.е. модуль спектральной плотности) от положения колебания на оси времени не зависит, т.к. комплексное число exp(-jwt₀) при любых t₀ имеет единичный модуль.

2.4.2 Изменение масштаба времени

Предположим, что исходный сигнал s(t) подвергнут преобразованию, связанному с изменением масштаба времени, т.е. роль времени t будет играть новая независимая переменная kt, где k – некоторое вещественное число. Если k > 1, то происходит «сжатие» исходного сигнала во времени; если же 0 < k < 1, то имеет место временное «растяжение» сигнала (рис. 2.3).

Оказывается, что если s(t) «S(w), то

s(kt) «(1/k) S(w/k). (2.32)

Это следует из:

при введении новой переменной интегрирования t = kt.

Рис. 2.3 – Сжатие сигнала при сохранении его формы и амплитуды.

Итак, при сжатии колебания в k раз на временной оси во столько же раз расширяется его спектр на оси частот. Модуль спектральной плотности при этом уменьшается в k раз. Очевидно, что при растяжении колебаний во времени имеет место сужение спектра и увеличение модуля спектральной плотности в 1/к раз.

2.4.3 Смещение спектра колебания

Применим преобразование Фурье (2.24) к произведению s(t)cos(w₀t + j₀), используя формулы Эйлера:

Первый интеграл в правой части есть не что иное, как спектральная плотность функции s(t) при частоте (w - w₀), а второй интеграл – при частоте (w + w₀). Поэтому полученное выше соотношение можно записать в форме:

(2.33)

где S(w) – спектральная плотность исходного колебания s(t).

Из выражения (2.33) вытекает, что расщепление спектра S(w) на две части, смещенные соответственно на +w₀ и -w₀, эквивалентно умножению функции s(t) на гармоническое колебание cos w₀t (при j₀ = 0).

2.4.4 Дифференцирование и интегрирование колебания

Пусть сигнал s(t) и его спектральная плотность S(w) заданы. Проанализируем новый сигнал, получаемый из исходного путем дифференцирования, и поставим цель найти его спектр. Оказывается, что справедлива формула:

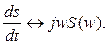(2.34)

Для доказательства необходимо вычислить преобразование Фурье от производной непосредственно:

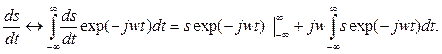
Внеинтегральное слагаемое обращается в нуль, поскольку s®0 при t ® ±¥ (условие интегрируемости сигнала). В результате получаем выражение (2.34).

При дифференцировании скорость изменения сигнала во времени обычно возрастает. Как следствие, спектр производной имеет большие значения в области высоких частот по сравнению со спектром исходного сигнала.

Формула (2.34) обобщается на случай спектра производной n-го порядка. Легко увидеть, что

(2.35)

Итак, дифференцирование сигнала во временной области эквивалентно простой алгебраической операции умножения спектральной плотности на множитель jw. Поэтому принято говорить, что мнимое число jw играет роль оператора дифференцирования, действующего в частотной области.

Во многих радиотехнических устройствах находят применение так называемые интеграторы – физические системы, работающие по следующему принципу: мгновенное значение сигнала на их выходе равно интегралу от функции, описывающей входное воздействие. Если и_вх и и_вых – соответственно сигналы на входе и выходе идеального интегратора, то

Между спектральной плотностью сигнала s(t) и значением его определенного интеграла с переменным верхним пределом существует связь:

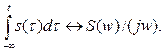(2.36)

Для доказательства следует заметить, что и воспользоваться формулой (2.34).

Таким образом, множитель 1/(jw) выступает как оператор интегрирования в частотной области.

2.4.5 Сложение и произведение двух колебаний

Так как преобразование Фурье, определяющее спектральную плотность заданной функции времени, является линейным преобразованием, то, очевидно, что при сложении колебаний s₁(t), s₂(t),..., обладающих спектрами S₁(w), S₂(w),..., суммарному колебанию s(t) = s₁(t) + s₂(t) +... соответствует спектр, являющийся их суммой: S(w) = S₁(w) + S₂(w) +....

Однако спектр произведения сигналов не равен произведению спектров, а выражается некоторым специальным интегральным соотношением между спектрами сомножителей.

Пусть v(t), u(t) - два сигнала, для которых установлены соответствия u(t) «U(w), v(t) «V(w). Образуем произведение этих сигналов: s(t) = u(t) v(t) и вычислим его спектральную плотность:

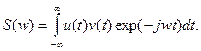(2.37)

Применив обратное преобразование Фурье, выразим сигнал v(t) через его спектр и подставим результат в (2.37):

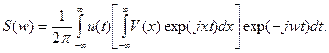
Изменив порядок интегрирования, будем иметь:

Заключенный в квадратные скобки интеграл представляет собой спектральную плотность функции u(t) при частоте (w-x), т.е. U(w-x). Следовательно, спектр произведения двух сигналов равен

(2.38)

Интеграл в правой части называется сверткой функций U и V. Операция свертки обозначается как V(w)*U(w). Операция свертки коммутативна, т.е. допускает изменение порядка следования преобразуемых функций: V(w)*U(w) = U(w)*V(w).

Можно показать, что произведению двух спектров U(w)V(w) = S(w) соответствует функция времени s(t), являющаяся сверткой функций u(t) и v(t):

(2.39)

2.4.6 Взаимная заменяемость w и t в преобразованиях Фурье

Обратимся к общему выражению (2.24) и выясним характер функции S(w) для различных функций s(t).

1. Пусть s(t) есть функция, четная относительно t. Записывая ППФ (2.24) через тригонометрические функции в виде

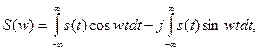
легко убедиться, что при четности s(t) второй интеграл равен нулю, так как произведение s(t)sinwt является функцией, нечетной относительно t, а пределы интегрирования симметричны. Таким образом, при s(t), четной относительно t, функция S(w), определяемая первым интегралом, есть функция вещественная и четная относительно w.

1. Если s(t) нечетна относительно t, то в нуль обращается первый интеграл и

В этом случае S(w) – нечетная и чисто мнимая функция w.

3. Если s(t) не является четной или нечетной функцией относительно t, то ее можно разложить на две функции: четную s₁(t) и нечетную s₂(t). При этом S(w) представляет полную комплексную функцию, причем действительная ее часть четна, а мнимая нечетная относительно w.

Из п. 1 вытекает, что при четной функции s(t) можно произвольно выбирать знак перед t в обратном преобразовании Фурье (2.25); выберем знак минус и запишем формулу (2.25) в виде:

Произведем теперь в последнем интеграле замену переменной интегрирования w на t и параметра t на w. Тогда левая часть должна быть записана в виде функции от w:

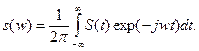
Но интеграл в последнем выражении можно рассматривать как спектральную плотность новой функции S(t), полученной путем замены w на t в выражении спектральной плотности колебания s(t). Обозначим эту новую спектральную плотность через S’(w). Тогда S’(w) = 2ps(w).

Этот результат показывает, что переменные w и t в преобразованиях Фурье взаимно заменимы: если колебанию (четному) s(t) соответствует спектр S(w), то колебанию S(t) соответствует спектр 2ps(w).

2.4.7 Свойство инверсии аргумента

В силу того, что действительная часть A(w) функции спектральной плотности является четной функцией частоты, а ее мнимая часть B(w) – нечетной (см. предыдущее свойство), будет справедлива следующая закономерность.

Если сигналу s(t) соответствует его спектральная плотность S(w), то сигналу с инверсным аргументом s(-t) будет соответствовать комплексно-сопряженное значение спектральной плотности S*(w).

Дата добавления: 2014-01-07