Примеры вычисления работы

Рассмотренные ниже при­меры дают результаты, которыми можно непосредственно пользо­ваться при решении задач.

1) Работа силы тяжести. Пусть точка М, на которую действует сила тяжести 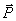, перемещается из положения М_­0 (x­₀, у₀, z₀) в положение M₁ (х₁, у₁, z₁). Выберем оси координат так, чтобы ось Oz была направлена вертикально вверх (рис.19).

Рис.19

Тогда Р _x=0, Р _y=0, P _z= - Р. Подставляя эти значения и учитывая перемен­ную интегрирования z:

.

Если точка M ₀ выше М ₁, то 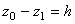, где h -величина вер­тикального перемещения точки;

Если же точка M ₀ ниже точки M ₁ то .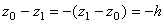

Окончательно получаем: .

Следовательно, работа силы тяжести равна взятому со зна­ком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной. Из полученного результата следует, что работа силы тяжести не зависит от вида той траектории, по которой перемещается точка ее приложения.

Силы, обла­дающие таким свойством, назы­ваются потенциальными.

2) Работа силы упругости. Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к свободному концу некоторой пружины (рис.20,а). Отметим на плоскости точкой О поло­жение, занимаемое концом пружины, когда она не напряже­на (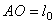 - длина ненапряженной пружины), и примем эту точку за начало координат. Если теперь оттянуть груз от равновесного положения О, удлинив пружину до величины , то на груз будет действовать сила упругости пружины F, направленная к точке О.

Рис.20

По закону Гука величина этой силы пропорциональна удлинению пружины . Так как в нашем случае , то по модулю .

Коэффициент с называется коэффициентом жесткости пружины. В технике обычно измеряют величину с в H/см, полагая коэф­фициент с численно равным силе, которую надо приложить к пру­жине, чтобы растянуть ее на 1 см.

Найдем работу, совершаемую силой упругости при перемещении груза из положения 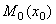в положение . Так как в данном случае , , то получим:

.

(Этот же результат можно получить по графику зависимости F от х (рис.20, б), вычисляя площадь 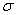заштрихованной на чертеже тра­пеции и учитывая знак работы.) В полученной формуле 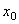представ­ляет собою начальное удлинение пружины 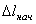, а конечное удлинение пружины 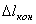. Следовательно,

,

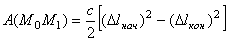т.е. работа силы упругости равна половине произведения коэффи­циента жесткости на разность квадратов начального и конеч­ного удлинений (или сжатий) пружины.

Работа будет положительной, когда , т. е. когда конец пружины перемещается к равновесному положению, и отрица­тельной, когда 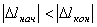, т.е. конец пружины удаляется от равновесия положения. Можно доказать, что формула ос­тается справедливой и в случае, когда пе­ремещение точки М не является прямо­линейным.

Таким образом, оказывается, что работа силы F зависит только от значе­ни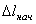й и 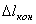и не зависит от вида траектории точки М. Следовательно, сила упругости также является потенциальной.

Рис.21

3) Работа силы трения. Рассмотрим точку, движущуюся по какой-нибудь шероховатой поверхности (рис. 21) или кривой. Действующая на точку сила трения равна по модулю fN, где f -коэффициент трения, а -нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно, F_тр=-fN и по формуле

.

Если величина силы трения постоянна, то , где s -длина дуги кривой М ₀ М ₁ по которой перемещается точка.

Таким образом, работа силы трения при скольжении всегда отрицательна. Величина этой работы зависит от длины дуги М ₀ М ₁. Следовательно, сила трения является силой непотенциальной.

4) Работа силы, приложенной к телу, вращающемуся вокруг неподвижной оси.

В этом случае (рис.22) точка приложения силы 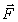движется по окружности радиуса r. Элементарная работа, по (1), 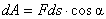, где .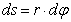

Рис.22

Поэтому .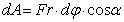

Но .

Это нетрудно установить, разложив силу на три составляющие (рис. 22). (Моменты сил и 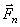равны нулю). Значит,

(2)

В частности, если момент силы относительно оси , работа силы при повороте тела на угол равна

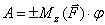. (3)

Знак работы определяется знаками момента силы и угла поворота. Если они одинаковы, работа положительная.

Из формулы (3) следует и правило определения работы пары сил. Если пара с моментом m расположена в плоскости перпендикулярной оси вращения тела, то ее работа при повороте тела на угол

. (4)

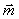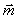Если же пара сил действует в плоскости не перпендикулярной оси вращения, то ее надо заменить двумя парами. Одну расположить в плоскости перпендикулярной оси, другую – в плоскости параллельной оси. Моменты их определяются разложением вектора момента по соответствующим направлениям: . Конечно работу будет совершать только первая пара с моментом , где – угол между вектором и осью вращения z,

. (5)

Дата добавления: 2014-01-07