Пример структурного анализа механизма

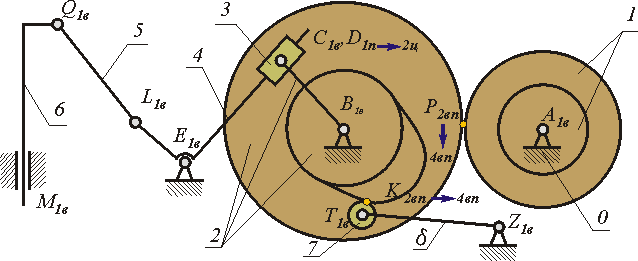
Рис. 2.8

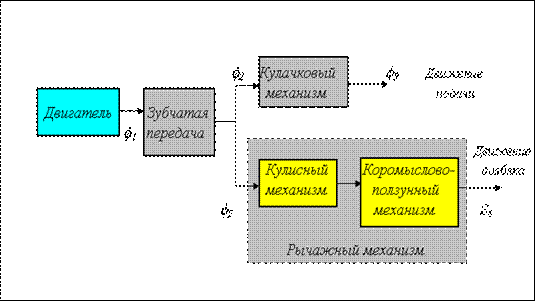
Функциональная схема на уровне типовых механизмов.

Рис. 2.9

На рис. 2.8 изображена структурная схема плоского механизма долбежного станка, а на рис.2.9 его функциональная схема на уровне типовых механизмов. Структурная схема механизма в соответствии с принятыми условными обозначениями изображает звенья механизма, их взаимное расположение, а также подвижные и неподвижные соединения между звеньями. На схеме звенья обозначены цифрами, кинематические пары - заглавными латинскими буквами. Цифры в индексах обозначения КП указывают относительную подвижность звеньев в паре, буквы - на вид пары, который определяется видом относительного движения звеньев (в - вращательное, п - поступательное, ц - цилиндрическое, вп - обозначает высшую пару в которой возможно относительное скольжение с одновременным перекатыванием). Схема на рис. 2.3 отражает структуру механизма в виде последовательного и параллельного соединения простых или типовых механизмов. В этом механизме вращательное движение вала двигателя φ₁ в согласованные движения подачи φ ₈ и долбяка S₆. При этом механическая энергия двигателя преобразуется: скоростные составляющие энергетического потока по величине уменьшаются, а силовые - увеличиваются. Структурные элементы (типовые механизмы) в этой схеме связаны между собой неподвижными соединениями - муфтами. Схема показывает: из каких простых механизмов состоит исследуемый, как эти механизмы взаимосвязаны между собой (последовательно или параллельно), как происходит преобразование входных движений в выходные (в нашем примере φ ₁ в φ ₈ и S₆).

Проведем структурный анализ данного механизма. Число подвижных звеньев механизма n=8, число кинематических пар p_i=12, из них для плоского механизма одноподвижных p₁=10 (вращательных p_1в=8, поступательных p_1п=2 и двухподвижных p₂=2. Число подвижностей механизма на плоскости:

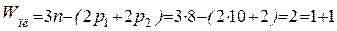
полученные две подвижности делятся на основную или реальную W₀ = 1 и местную W_м = 1. Основная подвижность определяет основную функцию механизма преобразование входного движения φ ₁ в два функционально взаимосвязанных φ ₈ и S₆. Местная (лишняя) обеспечивает выполнение вспомогательной функции: заменяет в высшей паре кулачок - толкатель трение скольжения трением качения. Число избыточных связей для механизма:

q^пл = W₀ + W_м - W^пл = 1 + 1 - 2 = 0;

Структурная классификация механизмов по Ассуру Л.В.

Для решения задач синтеза и анализа сложных рычажных механизмов профессором Петербургского университета Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации механизмы, не имеющие избыточных связей и местных подвижностей, состоят из первичных механизмов и структурных групп Ассура (см. рис. 2.4).

Рис. 2.10

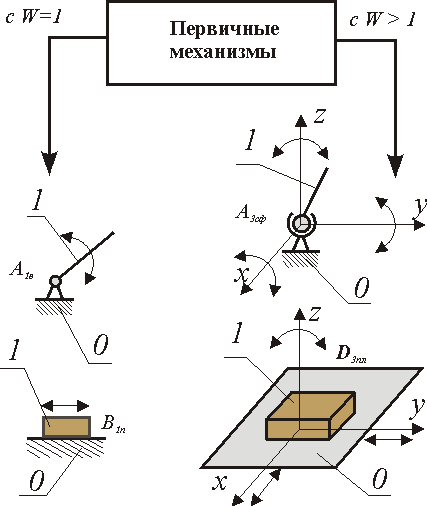
Под первичным (начальным) механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное) образующих кинематическую пару с одной W_пм= 1 или несколькими подвижностями. Примеры первичных механизмов даны на рис. 2.11.

Рис. 2.11

Структурной группой Ассура (или группой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (W_гр = 0).

Группы могут быть различной степени сложности. Структурные группы Ассура делятся на классы в зависимости от числа звеньев, образующих группу, числа поводков в группе, числа замкнутых контуров внутри группы.

В пределах класса (по Ассуру) группы подразделяются по числу поводков на порядки (порядок группы равен числу ее поводков). Конечные звенья групп Ассура, входящие в две кинематические пары, из которых одна имеет свободный элемент звена, называются поводками.

Механизмы классифицируются по степени сложности групп входящих в их состав. Класс механизма определяется наивысшим классом группы из входящих в него групп.

Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая ферма. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов.

Согласно теории Ассура в плоских механизмах группами являются кинематические цепи с низшими парами, которые удовлетворяют условию

W_гр = 3n_гр - 2p₅ = 0.

Решения этого уравнения в целых числах определяют параметры групп Ассура. Эти параметры, а также классы простейших групп Ассура по Ассуру и по Артоболевскому приведены в таблице 2.2.

Класс и порядок по Ассуру	1 кл. 2 пор.	3 кл. 3 пор.	4 кл. 2 пор.
Число звеньев группы nг р
Число кинематических пар p5

Несколько слов об историческом развитии классификации Ассура. В диссертационной работе Ассур разработал структурную классификацию для плоских рычажных шарнирных механизмов (т.е. для механизмов только с вращательными КП). В дальнейшем Артоболевский И.И. усовершенствовал и дополнил эту классификацию, распространив ее на плоские механизмы и с поступательными КП. При этом были изменены и принципы классификации.

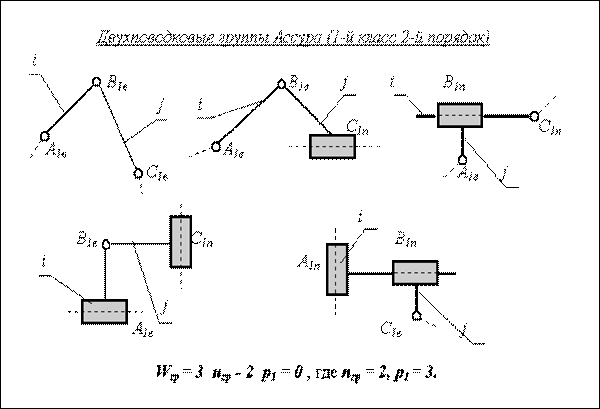
Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 2-го класса 2-го порядка. Число разновидностей таких групп для плоских механизмов с низшими парами невелико, их всего пять (см. рис. 2. 12) Для этих групп разработаны типовые методы структурного, кинематического и силового анализа (см. например, алгоритмы в [6] и программу DIADA).

Рис. 2. 12

Дата добавления: 2014-01-07