Способы представления и параметры

Анализ и расчет линейных цепей синусоидального тока

Переменный ток (напряжение) – это ток (напряжение), изменяющийся во времени либо по величине, либо по направлению, либо и по величине и по направлению. Частным случаем переменного тока является периодический ток.

Минимальный промежуток времени, по истечении которого повторяются мгновенные значения в том же порядке, называется периодом T [с] функции.

Синусоидальные токи и напряжения – это частный случай периодических токов и напряжений:

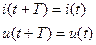
Величину обратную периоду называют частотой: 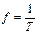[Гц].

Периодические токи и напряжения характеризуются:

- амплитудным значением (I_m, U_m) – максимальным значением за период;

- средним значением (I_0,, I_СР, U_{0 ,}, U_СР)

;

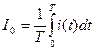- средневыпрямленным значением (I_{ср. в.}, U_{ср. в.})

;

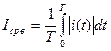- действующим значением (I, U, Е, J).

Действующим значением периодического тока 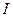называется такая величина постоянного тока, которая за период оказывает такое же тепловое действие, что и периодический ток.

Пусть

тогда мгновенная мощность переменного тока:

.

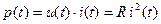Энергия, выделяющаяся за период в сопротивлении

.

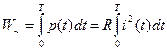Пусть по тому же сопротивлению R протекает постоянный ток, тогда мгновенная мощность постоянна: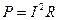

.

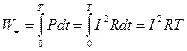Приравнивая энерги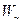и и 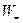, получим величину постоянного тока, оказывающего такое же тепловое действие, что и периодический ток, т.е. действующее значение периодического тока:

.

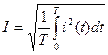Аналогично записывают формулу для действующего значения напряжения.

Активная мощность Р - это среднее значение мгновенной мощности за период:

.

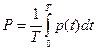Наиболее распространенным периодическим током является синусоидальный ток. Это связано с тем, что периодические сигналы, встречающиеся в электротехнике, можно представить в виде суммы синусоидальных функций кратных частот (ряд Фурье) и синусоидальный режим является наиболее экономичным режимом в цепях (минимальные потери).

В стандартной форме синусоидальные токи и напряжения записывают следующим образом:

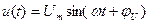
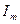и

- и 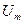- амплитудные значения,

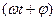- - называется фазой и показывает состояние, в котором находится изменяющаяся величина.

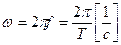- - угловая частота,

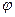- - начальная фаза, т.е. фаза в момент начала отсчета времени. На графике начальную фазу определяют от момента перехода синусоиды с отрицательных значений к положительным до начала координат.

Два колебания одинаковой частоты совпадают по фазе, если у них одинаковые начальные фазы; сдвинуты по фазе, если у них разные начальные фазы. Синусоида с большей начальной фазой опережает синусоиду с меньшей начальной фазой. Если сдвиг фаз равен 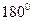говорят, что синусоиды в противофазе. Если сдвиг фаз 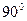, то синусоиды в квадратуре.

Для синусоидальных колебаний имеем:

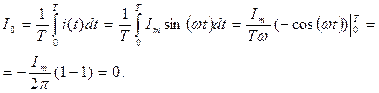
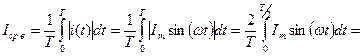
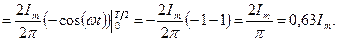
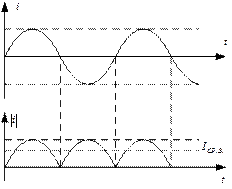
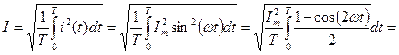
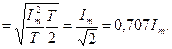
Интеграл от второго слагаемого =0 (см. вывод среднего значения).

В цепях синусоидального тока и напряжения мощность в каждый момент времени различна. Поэтому из равенства теплового действия выводят понятие активной мощности Р.

3.2 Элементы R,L,C в цепи синусоидального тока

Пусть через каждый элемент протекает синусоидальный ток .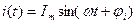

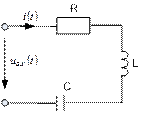
Тогда, согласно компонентным уравнениям и с учетом синусоидальности тока получаем:

;

;

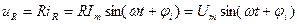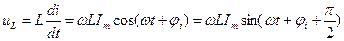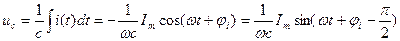
Напряжения на элементах в цепи синусоидального тока так же синусоидальны и имеют ту же частоту, но другие амплитуды и начальные фазы. Учитывая стандартную запись напряжения 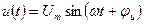, получаем

R	L	C

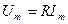
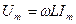
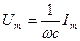
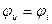
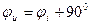
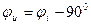
Напряжение на сопротивлении совпадает с током по фазе, напряжение на емкости отстает от тока на 90⁰, напряжение на индуктивности опережает ток на 90⁰.

Определим мгновенную и активную мощности на каждом элементе:

;

;

.

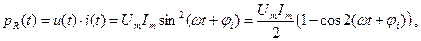
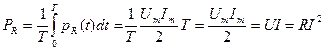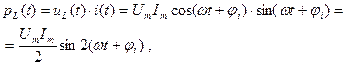
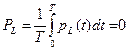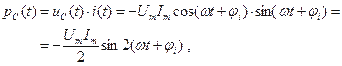
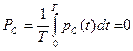для R

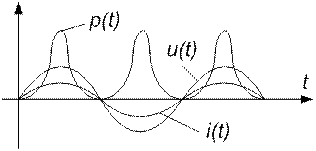
для L

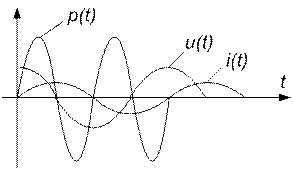
для C

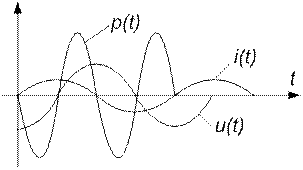
Таким образом, мгновенная мощность во всех элементах изменяется с двойной частотой тока. Однако мгновенная мощность в сопротивлении R содержит еще постоянную составляющую, поэтому активная мощность получается больше нуля. Индуктивность и емкость активной мощности не потребляют: половину периода мощность поступает от внешней цепи, а во вторую половину периода эти элементы отдают мощность во внешнюю цепь. В те моменты времени, когда индуктивность потребляет активную мощность, емкость генерирует её и наоборот.

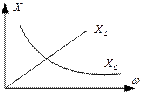
Так как сопротивление R потребляет активную мощность, то его называют активным сопротивлением. Индуктивность и емкость активной мощности не потребляют, поэтому их называют реактивными сопротивлениями и обозначают соответственно 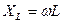[Oм] и 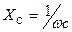[Oм].

Для расчета режима в цепи синусоидального тока можно записать систему уравнений по законам Кирхгофа, используя полученные соотношения между напряжением и током на элементах. Это будет система тригонометрических уравнений. Уравнения будут содержать синусоиды различной амплитуды и начальной фазы и необходимо проводить много тригонометрических преобразований, что не всегда удобно. Поэтому разработан специальный метод анализа режимов цепей синусоидального тока – метод комплексных величин или символический метод.

Дата добавления: 2014-01-07