Индуктивно связанные элементы цепи

Анализ и расчет цепей с индуктивной связью

Если по некоторой катушке k проходит ток , то вокруг неё создаётся магнитное поле и эту катушку характеризуют потокосцеплением . Более удобно катушку характеризовать индуктивностью:

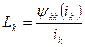. Если где-то расположена индуктивная катушка n, то часть магнитного поля k -ой катушки будет сцепляться с витками n -ой катушки. Этот эффект характеризуют потокосцеплением 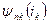. Удобнее этот эффект оценивать коэффициентом взаимной индуктивности : .

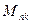Появление потокосцепления 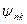на n -ой катушке, вызванное током, проходящем по k -ой катушке, называют индуктивной связью. В линейных цепях =.

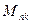Для характеристики степени связи катушек вводится коэффициент связи:

.

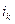Поделим и умножим на и 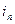. Учтем связь 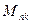=для линейных цепей. Получим: . Откуда .

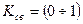, если катушки не связаны , и если сильно связаны, то .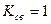

Т.о. при наличии нескольких индуктивно связанных катушек потокосцепление некоторой k -ой катушки будет равно:

.

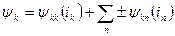Используя коэффициенты 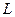и , получим .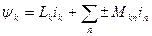

В соответствии с законом электромагнитной индукции изменяющийся во времени поток создаёт в катушке напряжение. Если все катушки неподвижны, то 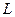и постоянны и изменяющиеся потоки получаются за счет изменяющихся токов:

,

где первое слагаемое называется напряжением самоиндукции, а второе – напряжением взаимоиндукции.

Т.о, явление взаимной индукции состоит в том, что ток одних катушек, изменяясь во времени, вызывает напряжение на других катушках, индуктивно связанных с первыми.

Если все токи синусоидальные, то можно воспользоваться символическим методом. От мгновенных значений токов и напряжений переходим к комплексам действующих или амплитудных значений, при этом 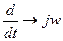, 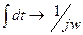. В нашем случае получаем: .

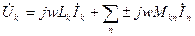Если катушки представляют собой реальные объекты, то с помощью правила правого винта легко установить какие потоки взаимоиндукции будут суммироваться с потоком самоиндукции, а какие вычитаться (аналогично для напряжения). Если мы работаем со схемами, то приходится применять значки и термины. Значками помечают одноимённые зажимы катушек.

Одноимёнными зажимами двух индуктивно связанных катушек называются такие два конца катушек, что если токи в катушках направлены одинаково относительно этих зажимов, то потоки и напряжения самоиндукции и взаимоиндукции будут суммироваться.

;

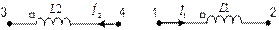
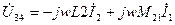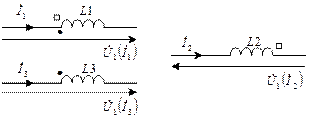
Пользуясь понятием одноимённых зажимов, можно расставить на схеме все напряжения и после этого составить уравнения по законам Кирхгофа, но это очень не удобно. Поэтому при расчёте цепей по второму закону Кирхгофа руководствуются специальным правилом, выводимым из понятия одноимённых зажимов: напряжение взаимоиндукции на катушке k, вызванное током катушки n, берется со знаком «+», если направление обхода контура с катушкой k и направление тока в ветви с катушкой n одинаково направлены относительно одноименных зажимов, иначе берется знак «-».

4.2 Расчёт режимов цепей с индуктивными связями

Нельзя сворачивать элементы цепи. Нельзя применять метод узловых потенциалов в той форме, в которой он был рассмотрен ранее, так как токи в этих схемах зависят не только от разности потенциалов концов ветвей, но и от наводимых в катушках напряжений взаимной индукции.

Метод уравнения Кирхгофа и метод контурных токов применять можно, при этом руководствуются следующим правилом: напряжение взаимоиндукции на катушке k, создаваемое током в катушке n берётся со знаком «+», если направление обхода катушки k и направление и направление тока в катушке n одинаково относительно одноимённых зажимов этих катушек.

Метод эквивалентного генератора можно применять, если нагрузка не имеет индуктивной связи с активным двухполюсником. В случае, когда метод применим, входное сопротивление активного двухполюсника следует искать также, как в схеме с управляемыми источниками.

- , при условии, что автономные источники заменены их внутренним сопротивлением, а к входным зажимам подключен дополнительный источник.

- .

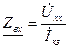Метод наложения и пропорциональных величин можно применять, так как это общие методы расчёта линейных цепей.

Пример: найти входное сопротивление в следующих схемах

Рис. 1

Рис. 2

В этом случае можно воспользоваться методом пробного источника. Подключим к каждой схеме пробные источники

1)

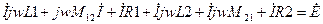
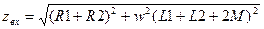
2)

Из примера видно, что модуль входного сопротивления в схеме рис. 1 больше, чем модуль входного сопротивления в схеме рис. 2. Первое соединение называется согласным, а второе встречным. На практике эту задачу можно использовать для экспериментального определения одноименных зажимов катушек.

Пример: найти входное сопротивление схемы

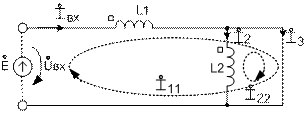
1. Воспользуемся методом пробного источника.

.

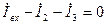
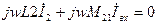
2. Воспользуемся методом контурных токов.

При нахождении уравнений методом контурных токов удобно сначала записывать уравнения без учёта индуктивных связей и только потом можно писать правую часть, после этого можно переписывать уравнения, приведя подобные члены.

, ,

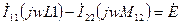
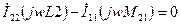
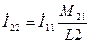
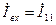Пример: записать систему уравнений Кирхгофа и метод контурных токов

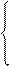
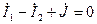
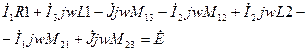
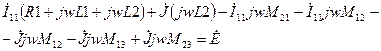
Рассмотренные примеры показывают, что даже в сравнительно простых цепях наличие индуктивных связей существенно усложняет запись уравнений и не даёт применять любые методы. Поэтому разработаны искусственные приёмы, позволяющие исключить в явной форме индуктивные связи.

4.3 Способы «замены» индуктивных связей

1) В любой цепи можно «устранить» индуктивные связи, введя управляемые источники определённой величины.

Например: в некоторой схеме есть две ветви 12 и 34, в которых есть катушки с индуктивной связью между собой:

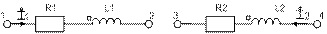
Запишем напряжение для каждой ветви:

и по полученным выражениям подберём схему замещения:

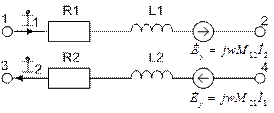
Теперь можно пользоваться любыми методами записи уравнений, но возникают все оговорки, связанные с наличием управляемых источников.

2) Замена индуктивных связей с помощью дополнительных индуктивностей (развязка индуктивных связей). Этот приём используют тогда, когда индуктивно связанные катушки стоят в ветвях, присоединённых к одному и тому же узлу.

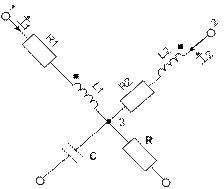
Катушки присоединены к общему узлу одноимёнными зажимами. Запишем уравнения для 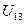и , искусственно преобразуем их, а после этого придумаем схему, которая соответствует придуманным уравнениям.

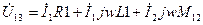
К правой части данного уравнения добавим и отнимем одну и ту же величину :

Аналогичным образом поступим для :

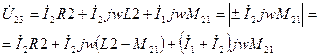
Полученным уравнениям соответствует следующая схема.

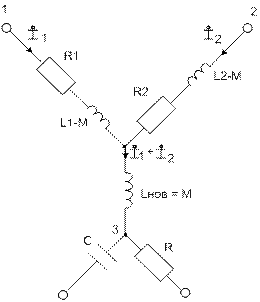
Рассмотрим случай, когда катушки присоединены к общему узлу разноимёнными зажимами:

Произведя точно такие же манипуляции, получим следующую схему замещения:

Пример: найти входное сопротивление

.

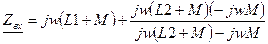Дата добавления: 2014-01-07