
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Процентная ставка. Простой и сложный проценты
|
|
|
|
Необходимой процедурой решения прикладных задач финансового менеджмента является оценка стоимости денег в различные моменты времени. Особенно это важно для анализа инвестиционных решений.
Стоимость денег с течением времени изменяется с учетом нормы прибыли на финансовом рынке, в качестве которой обычно выступает ставка процента. Поэтому вначале рассмотрим, как определяется этот финансовый показатель.
Ставка процента в общем случае - это выраженное в процентах отношение установленных дополнительных денежных выплат за определенный период к заимствованной или сберегаемой сумме.
Будем обозначать ставку процента символом  (%). Также часто в формулах финансовых вычислений фигурирует ставка процента
(%). Также часто в формулах финансовых вычислений фигурирует ставка процента  , выраженная десятичной дробью. Очевидно:
, выраженная десятичной дробью. Очевидно:
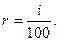
Ставке процента, как понятию, содержательно тождественны следующие термины: процентная ставка, норма процента, ссудный процент, процент.
В банковском секторе экономики используется целый комплекс различных видов процентных ставок.
Процентные (учетные) ставки, устанавливаемые Центральными банками, представляют собой один из важнейших инструментов, с помощью которого осуществляется внутренняя и внешняя экономическая политика. Поэтому основой ставок денежного рынка является официальная учетная ставка (фиксируемая) или текущие ставки по операциям Центрального банка. Эти ставки почти всегда ниже других ставок денежного рынка, поскольку операции по учету Центральным банком коммерческих векселей практически не сопряжены с риском.
Коммерческие банки устанавливают ставки процентов, ориентируясь на учетные ставки, принятые в Центральных банках своих стран. При этом крупные банки определяют минимальные или лучшие ставки по ссудам, предоставляемым первоклассным заемщикам.
Важное значение в структуре процентных ставок имеют проценты по вкладам банковских клиентов. Проценты, выплачиваемые банками их клиентам, всегда существенно ниже процентов по кредитам (за счет этой разницы формируется один из главных источников банковской прибыли — процентная маржа).
Экономической основой установления процентных ставок является соотношения рыночного спроса и предложения на финансовый капитал в денежной форме.
Финансовый (денежный) капитал - это деньги, вкладываемые предпринимателями в бизнес. Фирмы предъявляют спрос не только на физический капитал, но прежде всего на временно свободные денежные средства, которые можно потратить на приобретение капитальных благ.
Финансовый капитал возникает, поскольку домашние хозяйства не расходуют весь свой доход на текущее потребление, но часть его сберегают. Эти сбережения через финансовые рынки попадают к фирмам и используются ими для приобретения капитальных благ, т.е. для инвестиций. Используя капитал, источником которого являются сбережения домашних хозяйств, фирмы платят сберегателям ссудный процент, представляющий собой цену финансового капитала.
Предполагается, что финансовые рынки являются совершенно конкурентными. Иными словами, никто из отдельных сберегателей или фирм не в состоянии повлиять на процентную ставку, изменяя величину предложения своих сбережений либо свой спрос на них. Равновесная рыночная процентная ставка возникает в процессе конкуренции всех сберегателей и инвесторов.
Спрос фирм на финансовый капитал для инвестиций зависит от процентной ставки: чем она ниже, тем больше инвестиции. Предложение сбережений обычно положительно зависит от процентной ставки: чем выше процентная ставка, тем больше сбережения.
Отложим на рис. 1 по горизонтальной оси размеры инвестиций фирм (I) и сбережений домашних хозяйств (S), а по вертикальной — процентную ставку ( ) и отобразим функции спроса фирм на денежные средства для инвестиций (
) и отобразим функции спроса фирм на денежные средства для инвестиций ( ) и предложения сбережений домашними хозяйствами (
) и предложения сбережений домашними хозяйствами ( ).
).

Рис. 1. Равновесие на финансовом рынке
Точка пересечения этих двух функций дает нам равновесную процентную ставку ( ). При такой ставке финансовые рынки находятся в состоянии равновесия, ибо инвестиции равны сбережениям (
). При такой ставке финансовые рынки находятся в состоянии равновесия, ибо инвестиции равны сбережениям (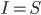 ).
).
Отдельная фирма-инвестор не может повлиять на рыночную процентную ставку, но принимает ее как заданную. Поэтому для определения инвестиций, осуществляемых данной фирмой, следует подставить рыночную процентную ставку в функцию инвестиционного спроса фирмы.
От процентной ставки зависит рентная цена капитала. Допустим, цена оборудования составляет 100 руб., срок его службы 5 лет, а процентная ставка равна 10% годовых. В этом случае владелец оборудования будет сдавать его в аренду минимум за 30 руб. в год, из которых 20 руб. будут возмещать ежегодный износ оборудования (100 руб./5 лет), а 10 руб. составят процент на денежный капитал (100 руб. х 0,1), вложенный владельцем в покупку оборудования. Поэтому минимальная рентная цена капитала равна сумме затрат на амортизацию и процента на капитал.
Таким образом, процентная ставка влияет на минимальную цену предложения капитала на рынке капитальных услуг.
Финансовые расчеты могут осуществляться на основе простого или сложного процента.
При использовании простого процента его начисление в обусловленный период осуществляется только на первоначально инвестированную сумму. Для этого используется следующая формула:

где:
 первоначальная сумма (стоимость) денежных средств;
первоначальная сумма (стоимость) денежных средств;
 количество интервалов, по которым осуществляется расчет процентных платежей;
количество интервалов, по которым осуществляется расчет процентных платежей;
 ставка процента, используемая для данного интервала (например,
ставка процента, используемая для данного интервала (например,
годового);
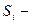 сумма доначислений по данной ставке процента за период в
сумма доначислений по данной ставке процента за период в  расчетных интервалов.
расчетных интервалов.
Рассмотрим примеры.
Пример 1.1.1. Пусть первоначальная сумма денежных средств равна:
 = 1000000 руб., а ставка процента
= 1000000 руб., а ставка процента  = 20% годовых. Определить, какую сумму получит вкладчик через 5 лет. Очевидно, она равна:
= 20% годовых. Определить, какую сумму получит вкладчик через 5 лет. Очевидно, она равна:
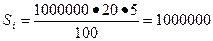 руб.
руб.
Если простой процент начисляется в течение периода времени, которое меньше года, формула (1) принимает вид:

или:

Где: 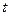 - количество дней начисления процента в течение года;
- количество дней начисления процента в течение года;
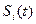 - сумма доначислений процента за
- сумма доначислений процента за 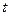 дней.
дней.
Если не сказано иное, обычно начисленный процент задается как процент в расчете на год. Тогда за 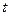 дней будет начислена только его часть, а именно:
дней будет начислена только его часть, а именно:
 или
или 
Финансовый год в первом случае принят равным 360, а в формуле (3) - 365 дням. Выбор формулы (2) или (3) зависит от того, с каким инструментом работает инвестор. Так, в банковской системе год считается равным 360 дням. Поэтому расчеты по начислению процентов по вкладам следует делать с помощью формулы (2). Расчеты по операциям с государственными краткосрочными облигациями осуществляются на базе, равной 365 дням. В этом случае используют формулу (3).
Пример 1.1.2.
Вкладчик размещает в банке 1000000 руб. под 20% годовых. Определить, какую сумму доначислений он получит через 300 дней. Она равна:
 руб.
руб.
В процессе анализа финансовые расчеты следует осуществлять на основе одного временного периода, т. е. 360 или 365 дней. Поэтому возникает необходимость перерасчета величины процента с одной временной базы на другую. Это можно сделать с помощью формул (4) и (5):


где:  - ставка процента на базе 365 дней;
- ставка процента на базе 365 дней;  - ставка процента на базе 360 дней.
- ставка процента на базе 360 дней.
Пример 1.1.3.
Пусть 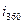 =20%. Тогда:
=20%. Тогда:

В примере процентная ставка на базе 365 дней равна 20, 28%, а для 360 дней - только 20%. Такой результат получается в связи с тем, что в первом случае предполагается начисление процентов дополнительно еще в течение 5 дней.
Если период начисления процентов измеряется в месяцах, то формулы (2) и (3) можно представить следующим образом:

Где: a - число месяцев, за которые начисляется процент;
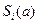 - дополнительная сумма, которую инвестор получит через а месяцев.
- дополнительная сумма, которую инвестор получит через а месяцев.
Пример 1.1.4.
Вкладчик размещает в банке 1000000 руб. под 20% годовых с месячным периодом доначислений. Определить, какую сумму доначислений он получит через 3 месяца ( ). С помощью (6) получаем, что она равна:
). С помощью (6) получаем, что она равна:
 руб.
руб.
При использовании сложного процента его начисление в обусловленный период осуществляется не только на первоначально инвестированную сумму, но также и на доначисления по процентам. Т.е. осуществляется капитализация процентов. Для этого используется следующая формула:
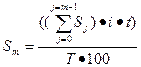 (7).
(7).
где:
 – годовая процентная ставка;
– годовая процентная ставка;
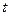 – количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов;
– количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов;
 – количество дней в календарном году (365 или 366);
– количество дней в календарном году (365 или 366);
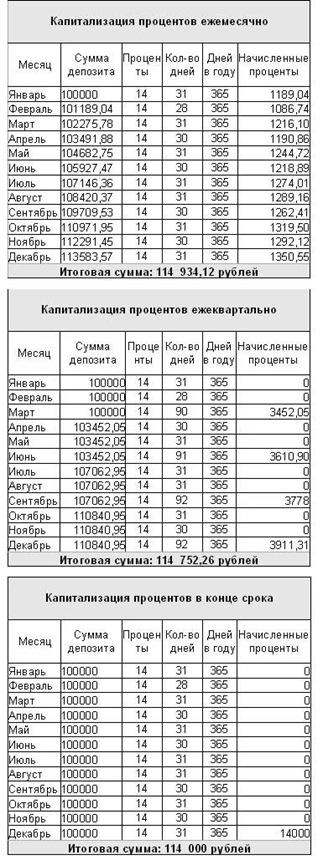
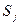 –
–  я сумма доначислений с учетом капитализации процентов;
я сумма доначислений с учетом капитализации процентов;
 – итоговая сумма доначислений по сложным процентам для
– итоговая сумма доначислений по сложным процентам для  интервалов, по которым осуществляется расчет процентных платежей. Рассмотрим примеры.
интервалов, по которым осуществляется расчет процентных платежей. Рассмотрим примеры.
Пример 1.1.5. (см. таблицу 1).
В этом случае, мы применяем формулу сложных процентов, так как капитализация процентов происходит ежемесячно. Поскольку  руб., получаем в первом месяце:
руб., получаем в первом месяце:
Янв:  = (100000х14х31/365)/100;
= (100000х14х31/365)/100;
 =1189,04 руб.
=1189,04 руб.
Далее, получившуюся сумму, мы прибавляем к нашему первоначальному вкладу. Получаем:  =101189,04 руб. Так выглядит ежемесячная капитализация. Дальше февраль рассчитываем аналогичным образом, не забывая про то, что в феврале 28 или 29 дней.
=101189,04 руб. Так выглядит ежемесячная капитализация. Дальше февраль рассчитываем аналогичным образом, не забывая про то, что в феврале 28 или 29 дней.
Фев:  =(101189.04х14х28/365)/100
=(101189.04х14х28/365)/100
 =1086,74 руб. (сумма получилась меньше, так как в феврале было меньше дней, чем в предыдущем месяце). Прибавляем 1086.74 к 101189,04:
=1086,74 руб. (сумма получилась меньше, так как в феврале было меньше дней, чем в предыдущем месяце). Прибавляем 1086.74 к 101189,04: = 102275,78 руб. И так далее…
= 102275,78 руб. И так далее…
Пример 1.1.6. (см. таблицу 2).
В этом случае капитализация процентов производится ежеквартально. Применяем формулу сложных процентов и действуем по аналогии с первым примером. Здесь следует обратить внимание, что многие при расчете ежеквартальной капитализации совершают распространенную ошибку, подставляя в формулу (7) неправильное количество дней. Нужно ставить не 30 или 31 день, по количеству дней в месяце, а количество дней за общий календарный период. Для этого мы суммируем количество дней за 3 месяца квартала. В первом квартале – это 90, либо 91 день. Во втором – 91 и т.д.
1 кв.:  =(100000х14х90/365)/100
=(100000х14х90/365)/100
 =3452,05 руб. Прибавляем это к первоначальной сумме. Получаем 103452,05 руб. Далее аналогично.
=3452,05 руб. Прибавляем это к первоначальной сумме. Получаем 103452,05 руб. Далее аналогично.
Пример 1.1.7. (см. таблицу 3).
Капитализация процентов в этом случае производится в конце срока. Для этого применяется формула расчета простых процентов (1).
 =(100000х14х365/365)/100;
=(100000х14х365/365)/100;
 =14000 руб.
=14000 руб.
С применением сложных процентов доходы кредитора начинают расти во времени не в прямой пропорциональной, как при простых процентах, а в степенной зависимости. Начисляемые, но не выплачиваемые сложные проценты присоединяются к сумме основного долга, вследствие чего происходит начисление процентов на проценты. Постоянный рост исходной суммы для начисления процентов таким образом дает эффект ускорения наращения процентного дохода.
Для кредитора сложные проценты - это возможность сохранить текущую стоимость имеющихся средств, необходимых к определенному моменту в будущем. Для заемщика это способ сэкономить на операционных затратах, увеличить стабильность ресурсной базы за счет увеличения сроков заимствования средств.
1.2. Наращение и дисконтирование стоимости
Концепция стоимости денег во времени играет основополагающую роль в практике финансовых вычислений. Она предопределяет необходимость учета фактора времени в процессе осуществления любых долгосрочных финансовых операций путем оценки и сравнения стоимости денег при начале финансирования со стоимостью денег при их возврате в виде будущей прибыли, амортизационных отчислений, основной суммы долга и т.д.
В процессе сравнения стоимости денежных средств при планировании их потоков в продолжительном периоде времени используется два основных понятия - будущая стоимость денег или их настоящая стоимость.
Будущая стоимость денег представляет собой сумму инвестированных в настоящий момент средств, в которую они превратятся через определенный период времени с учетом определенной ставки процента. Определение будущей стоимости денег характеризует процесс наращения их стоимости (компаундинг), который состоит в присоединении к их первоначальной сумме начисленной суммы процентов.
Настоящая стоимость денег представляет собой сумму будущих денежных средств, приведенную с учетом определенной ставки процента к настоящему периоду времени. Определение настоящей стоимости денег характеризует процесс дисконтирования их стоимости, который представляет операцию, обратную наращению, осуществляемую путем изъятия из будущей стоимости соответствующей суммы процентов (дисконтной суммы или «дисконта»).
При проведении финансовых вычислений, связанных с оценкой стоимости денег во времени, процессы наращения или дисконтирования стоимости могут осуществляться как по простым, так и по сложным процентам, которые мы уже рассмотрели в предыдущем параграфе.
При использовании простого процента в результате наращения стоимости будущая стоимость вклада  в момент времени
в момент времени 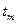 определяется по формуле:
определяется по формуле:

где:
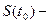 первоначальная сумма (стоимость) денежных средств на момент времени
первоначальная сумма (стоимость) денежных средств на момент времени  ;
;
 количество интервалов продолжительностью
количество интервалов продолжительностью  (например, месяц, квартал, год), по которым осуществляется расчет процентных платежей;
(например, месяц, квартал, год), по которым осуществляется расчет процентных платежей;
 ставка процента, используемая для данного интервала
ставка процента, используемая для данного интервала  (выраженная в процентах);
(выраженная в процентах);
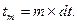
Множитель  называется коэффициентом наращения суммы простых процентов. По определению его значение всегда должно быть больше единицы.
называется коэффициентом наращения суммы простых процентов. По определению его значение всегда должно быть больше единицы.
Рассмотрим примеры.
Пример 1.2.1. Определить будущую стоимость вклада в 100000 руб. через три года, если годовая ставка процента составляет 10% и начисление производится по схеме простых процентов. Здесь: 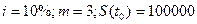 руб. Используя формулу (8), получаем:
руб. Используя формулу (8), получаем:
 руб.
руб.
Пример 1.2.2. Определить значение коэффициента наращения суммы простых процентов, если годовая ставка процента составляет 8%, а начисления производятся в течении 5 лет. Запишем исходные данные:  С помощью формулы (9) получаем:
С помощью формулы (9) получаем:

Теперь рассмотрим, как вычисляется будущая стоимость вклада  в результате наращения стоимости по сложным процентам.
в результате наращения стоимости по сложным процентам.
Если начисление сложных процентов производится один раз в год, то через  лет будущая стоимость составит:
лет будущая стоимость составит:

В этом случае коэффициент наращения определяется по формуле:
 (11).
(11).
Пример 1.2.3. Определить будущую стоимость вклада в 1000000 руб. через 5 лет, если ставка процента – 20% годовых, а начисление производится по схеме сложных процентов.
 руб.
руб.
Сложный процент может начисляться чаще, чем один раз в год. Например, раз в полгода (или два раза в год), раз в квартал, месяц и т. д. В этом случае формула (10) принимает вид:
 (12).
(12).
где:
 годовая ставка процента;
годовая ставка процента;
 количество начислений сложного процента в течении года.
количество начислений сложного процента в течении года.
В этом более общем случае коэффициент наращения определяется по формуле:
 (13).
(13).
Пример 1.2.4.
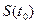 = 1000000 руб.,
= 1000000 руб.,  = 20%. Определить сумму, которую вкладчик получит в конце пятого года, если сложный процент начисляется: а) ежеквартально; б) ежемесячно.
= 20%. Определить сумму, которую вкладчик получит в конце пятого года, если сложный процент начисляется: а) ежеквартально; б) ежемесячно.
Применяя формулу (12) для значений параметров: 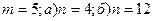 , получаем:
, получаем:
 руб.
руб.
 руб.
руб.
Как видно из данного примера, чем чаще периодичность начисления сложного процента, тем большую сумму получит инвестор за тот же период времени при одинаковой годовой процентной ставке.
Чтобы сравнить суммы денег во времени, их необходимо привести к единому временному знаменателю. В практике финансовых расчетов принято приводить суммы средств, которые получит инвестор, к сегодняшнему дню, т. е. начальной точке отсчета 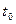 . Такая процедура называется дисконтированием.
. Такая процедура называется дисконтированием.
Если используются расчеты по простым процентам, настоящая стоимость денежных средств 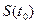 на основании формулы (8) определяется следующим образом:
на основании формулы (8) определяется следующим образом:

Используемый множитель  (15) называется коэффициентом дисконтирования. Его значение всегда меньше единицы.
(15) называется коэффициентом дисконтирования. Его значение всегда меньше единицы.
При расчете настоящей стоимости денежных средств в процессе дисконтирования по сложным процентам, если их начисление производится один раз в год в течение  лет, используется следующая формула:
лет, используется следующая формула:

В этом случае коэффициент дисконтирования определяется по формуле:
 (17).
(17).
Пример 1.2.5.
Инвестор желал бы через пять лет получить на своем счете 5 млн. руб. Банк начисляет 20% годовых. Определить, на какую сумму необходимо вкладчику сегодня открыть счет. С помощью формулы (16) определяем:
 руб.
руб.
Если начисление сложных процентов осуществляется 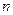 раз в год в течение
раз в год в течение  лет, расчете настоящей стоимости денежных средств осуществляется по формуле:
лет, расчете настоящей стоимости денежных средств осуществляется по формуле:

При этом коэффициент дисконтирования в этом случае рассчитывается так:
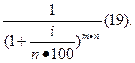
При оценке стоимости денег во времени по сложным процентам необходимо иметь в виду, что на результат оценки оказывает большое влияние не только используемая ставка процента, но и число интервалов выплат в течение одного и того же общего платежного периода. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большим числом интервалов в течение предусмотренного периода платежа.
Коэффициенты наращения и дисконтирования суммы сложных процентов положены в основу специальных таблиц финансовых вычислений, с помощью которых при заданных размерах ставки процента и количества платежных интервалов можно легко вычислить настоящую или будущую стоимость денежных средств по сложным процентам.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 10001; Нарушение авторских прав?; Мы поможем в написании вашей работы!