Простейшая биноминальная модель

Определение стоимости опциона

Производным финансовым инструментом «европейского типа» называется финансовый инструмент, если существует платежная функция F(z), такая, что в заданный момент времени Т стоимость производного инструмента равна 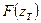, где 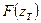- стоимость исходных активов в момент Т.

Платежной функцией производного финансового инструмента «европейского типа» называется функция F(z), удовлетворяющая всем вышеперечисленным условиям.

Платежные функции европейских опционов «колл» и «пут» имеют вид:

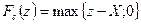[50]

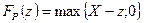[51]

При оценке стоимости производных финансовых инструментов предположим, что выполняются следующие условия:

· рассматриваемые рынки являются совершенными;

· неограниченно можно кредитовать и брать средства в долг под соответствующие по срокам безрисковые процентные ставки.

· отсутствуют прибыльные арбитражные возможности.

Предположим, что:

цена исходных активов в текущий момент t известна и равна S;

к моменту времени Т цена исходных активов поднимется до величины 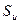с вероятностью, равной р, или опускается до величины 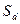с вероятностью, равной 1-р, где u и d – некоторые числа, причем u>1 и 0< d<1.

Простейшая модель изменения цены исходного актива может быть представлена в следующем виде (рис. 24).

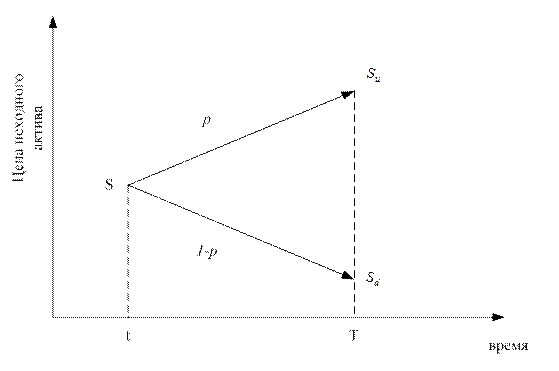
Рис. 24. Простейшая модель эволюции цены базового актива

Стоимость финансового инструмента «европейского типа», производного от исходных активов с постоянной дивидендной доходностью, равной q, определяется по формуле:

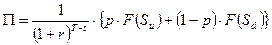[52]

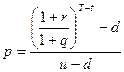где [53]

Пример. Текущая цена английского фунта стерлингов равна 1,8 долл. Через 4 месяца она может подняться до 1,82 долл. или снизится до 1,75 долл. Оцените стоимость четырехмесячного европейского опциона «колл» на 1000 фунтов, если безрисковые процентные ставки на 4 мес. в США и Великобритании равны 6 и 4% соответственно, а цена исполнения опциона – 1,81 долл.

Решение

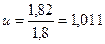
Согласно условию задачи, r = 0,06 и q= 0,04, T-t= 4/12.

Находим вероятность роста:

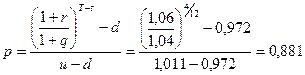
Следовательно, (1 - р)=0,119.

Для европейского опциона «колл» платежная функция будет иметь следующий вид:

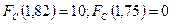
В этом случае стоимость опциона будет равна:

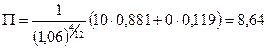долл.

Дата добавления: 2014-01-07