Доходность портфеля облигаций

Предположим, что на рынке присутствуют облигации l видов, стоимость которых в данный (нулевой) момент равны соответственно 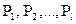. Будем считать, что данные облигации можно покупать в любом количестве.

Инвестор, затратив на покупку сумму 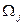на покупку облигаций j -го вида (j = 1,2,3, …, l), сформирует портфель облигаций

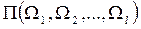
стоимостью 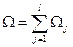[75]

Обозначим через 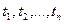моменты времени, когда хоты бы по одной из облигаций производится платеж.

Если 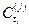- платеж по j-той облигации в момент времени 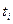(i = 1,2, …, n), то инвестор покупая портфель облигаций 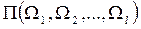, приобретает право на получение следующего потока платежей:

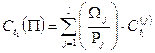
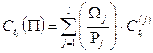[76]

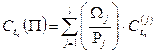
Следовательно, по своим инвестиционным качествам портфель облигаций 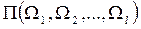эквивалентен одной единственной облигации стоимостью 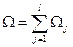, по которой в моменты 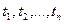производятся платежи .

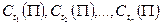Пример. Даны облигации трех видов, потоки платежей по которым представлены в табл. 8.

Таблица 8

Исходные данные

Облигация	Платеж по срокам, долл.
	0,5		1,5
А	-100
В	-100	-		-
С	-105			-	-

Определите поток платежей от портфеля П (200, 400, 500).

Решение

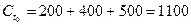
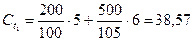
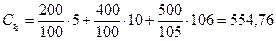
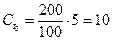
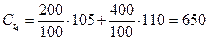
Таким образом, поток платежей от портфеля П (200,400,500) будет иметь следующий вид:

Срок, годы		0,5		1,5
Платеж, долл.	-1100	38,57	554,76

Внутренней доходностью портфеля облигаций П называется внутренняя доходность облигации, эквивалентной портфелю П.

Пример. Найдем внутреннюю доходность портфеля П исходя из условия предыдущей задачи при начислении процентов дважды в год.

Решение. Для нахождения внутренней доходности портфеля необходимо найти внутреннюю доходность облигации, эквивалентной портфелю облигаций П. Для этого необходимо решить следующее уравнение:

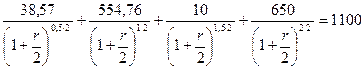
Данное равенство выполняется при r = 8,92% годовых.

Наряду с внутренней доходностью портфеля часто рассматривают средневзвешенную доходность портфеля облигаций.

Средневзвешенной доходностью портфеля облигаций 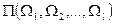называется взвешенная по стоимости сумма доходностей облигаций этого портфеля, т.е.

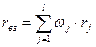[77]

где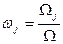

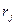- внутренняя доходность облигации j -го вида, j = 1,2,3,…, l

Пример. Определить средневзвешенную доходность портфеля из предыдущего примера при начислении процентов два раза в год.

Решение

Предварительно необходимо найти внутренние доходности всех облигаций, входящих в портфель П (200, 400, 500).

Внутренняя доходность первой облигации:

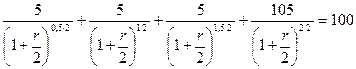
Решив это уравнение, получим r = 10%.

Внутренняя доходность второй облигации:

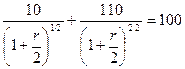
Решив это уравнение, получим r 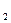= 9,76%.

Внутренняя доходность третьей облигации:

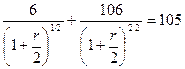
Решив это уравнение, получим r = 6,74%.

Следовательно, средневзвешенная доходность портфеля составит:

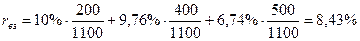
Из всех примеров следует, что внутренняя доходность портфеля может значительно отличаться от его средневзвешенной доходности. Однако средневзвешенная доходность будет совпадать с внутренней доходностью портфеля облигаций, если все облигации, входящие в портфель, имеют одну и ту же доходность.

Дата добавления: 2014-01-07