Математическая логика

Определение. Если при стремлении к нулю шага разбиения кривой АВ интегральные суммы имеют конечный предел, то этот предел называется криволинейным интегралом по переменной х от функции P(x, y, z) по кривой АВ в направлении от А к В.

Криволинейный интеграл второго рода, т.е. интеграл по координатам отличается от криволинейного интеграла первого рода, т.е. по длине дуги тем, что значение функции при составлении интегральной суммы умножается не на длину частичной дуги, а на ее проекцию на соответствующюю ось. (В рассмотренном выше случае – на ось ОХ).

Вообще говоря, криволинейные интегралы могут считаться также и по переменным у и z.

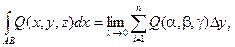
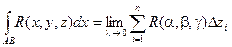
Сумму криволинейных интегралов также называют криволинейным интегралом второго рода.

Свойства криволинейного интеграла второго рода.

1) Криволинейный интеграл при перемене направления кривой меняет знак.

2)

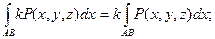
3)

4)

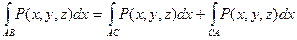
5) Криволинейный интеграл по замкнутой кривой L не зависит от выбора начальной точки, а зависит только от направления обхода кривой.

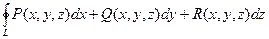
Направление обхода контура L задается дополнительно. Если L – замкнутая кривая без точек самопересечения, то направление обхода контура против часовой стрелки называется положительным.

6) Если АВ – кривая, лежащая в плоскости, перпендикулярной оси ОХ, то

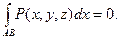
Аналогичные соотношения справедливы при интегрировании по переменным у и z.

Теорема. Если кривая АВ – кусочно- гладкая, а функции P(x, y, z), Q(x, y, z) и

R(x, y, z) – непрерывны на кривой АВ, то криволинейные интегралы

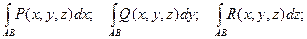
существуют.

Вычисление криволинейных интегралов второго рода производится путем преобразования их к определенным интегралам по формулам:

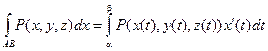
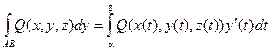
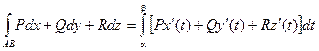
В случае, если АВ – плоская кривая, заданная уравнением y = f(x), то

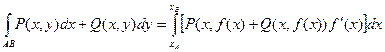
Пример. Вычислить криволинейный интеграл 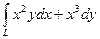. L – контур, ограниченный параболами 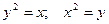. Направление обхода контура положительное.

Представим замкнутый контур L как сумму двух дуг L₁ = x² и

Формула Остроградского – Грина.

(Остроградский Михаил Васильевич (1861-1862) – русский математик,

академик Петерб. А.Н.)

(Джордж Грин (1793 – 1841) – английский математик)

Иногда эту формулу называют формулой Грина, однако, Дж. Грин предложил в 1828 году только частный случай формулы.

Формула Остроградского – Грина устанавливает связь между криволинейным интегралом и двойным интегралом, т.е. дает выражение интеграла по замкнутому контуру через двойной интеграл по области, ограниченной этим контуром.

Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.

y

y = y₂(x)

D

A

C

B

y= y₁(x)

0 x₁ x₂ x

Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:

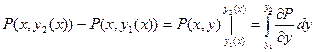
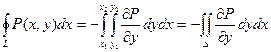
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:

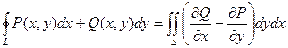
Эта формула называется формулой Остроградского – Грина.

Формула Остроградского – Грина справедлива и в случае многосвязной области, т.е. области, внутри которой есть исключенные участки. В этом случае правая часть формулы будет представлять собой сумму интегралов по внешнему контуру области и интегралов по контурам всех исключенных участков, причем каждый из этих контуров интегрируется в таком направлении, чтобы область D все время оставалась по левую сторону линии обхода.

Пример. Решим пример, рассмотренный выше, воспользовавшись формулой Остроградского – Грина.

Формула Остроградского – Грина позволяет значительно упростить вычисление криволинейного интеграла.

Криволинейный интеграл не зависит от формы пути, если он вдоль всех путей, соединяющих начальную и конечную точку, имеет одну и ту же величину.

Условием независимости криволинейного интеграла от формы пути равносильно равенству нулю этого интеграла по любому замкнутому контуру, содержащему начальную и конечную точки.

Это условие будет выполняться, если подынтегральное выражение является полным дифференциалом некоторой функции, т.е. выполняется условие тотальности.

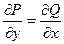
Определение 1. Логика – анализ методов рассуждений.

Рассмотрим два вывода: 1) Все люди смертны. Сократ – человек, следовательно, Сократ смертен. 2) Все кролики любят морковь. Ушастик – кролик, следовательно, Ушастик любит морковь.

Оба вывода имеют одну и ту же форму: все А суть В, С есть А, следовательно, С есть В.

Логик желает знать, вытекает ли истинность заключения из истинности посылок.

Основная задача логика – систематическая формализация и каталогизация правильных способов рассуждений.

Главная цель математической логики – дать точное и адекватное определение понятия «математическое доказательство».

Определение 2. Алфавитом 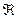называется любое непустое множество. Элементы этого множества называются символами алфавита.

Определение 3. Словом в алфавите называется произвольная, конечная (возможно, пустая) последовательность символов из .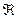

Определение 4. Произведением слов a и b называется слово ab. Предложение – произвольная конечная последовательность слов.

Определение 5. Рассмотрим алфавит: , где 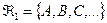, , 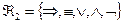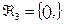. Символы из 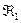называются переменными высказываниями или пропозициональными буквами. Символы из 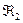называются логическими связками или пропозициональными связками. Символы из (скобки, запятые) называются вспомогательными символами.

п. 1. Высказывания (пропозициональные буквы)

Истина и ложь – слова, которые называются значениями истинности.

Определение 6. Высказывание – утвердительное предложение, про которое можно сказать истинно оно или ложно.

Например, «идет дождь» – высказывание, «пойдем обедать» – не высказывание.

Высказывание может быть выражено с помощью слов, а также с помощью математических, химических и других знаков.

Не являются высказываниями 1) восклицательные и вопросительные предложения; 2) также определения (они устанавливают названия и понятия некоторого объекта); 3) также предложения типа: «он сероглаз или » (не указано, о каком человеке идет речь, при каких х рассматривается неравенство; такие предложения с неизвестной переменной называются неопределенными высказываниями).

Например, «некоторые люди – сероглазы» – высказывание, «для всех справедливо неравенство » – высказывание, причем 1) – истинное, а 2) – ложное.

Высказывания, которые можно разложить на части – сложные, нельзя – простые.

Из высказываний путем соединения их различными способами можно составлять новые, более сложные высказывания.

Иногда бывает удобнее представлять некоторые словесные выражения – высказывания, посредством логических символов, которые называются кванторами.

Дата добавления: 2014-01-07