Меры информации синтаксического уровня

Меры информации

Для измерения информации на синтаксическом уровне вводятся два параметра: объем информации (данных) – V_Д (объемный подход) и количество информации — I (энтропийный подход).

Объем информации V_Д. При реализации информационных процессов информация передается в виде сообщения, представляющего собой совокупность символов какого-либо алфавита. Если количество информации, содержащейся в сообщении из одного символа, принять за единицу, то объем информации (данных) V_Д в любом другом сообщении будет равен количеству символов (разрядов) в этом сообщении.

Так, в десятичной системе счисления один разряд имеет вес, равный 10, и соответственно единицей измерения информации будет дит (десятичный разряд). В этом случае сообщение в виде n -разрядного числа имеет объем данных V_Д = п дит. Например, четырехразрядное число 2003 имеет объем данных V_Д = 4 дит.

В двоичной системе счисления один разряд имеет вес, равный 2, и соответственно единицей измерения информации будет бит (bit (binary digit) - двоичный разряд). В этом случае сообщение в виде n -разрядного числа имеет объем данных V_Д = п бит. Например, восьмиразрядный двоичный код 11001011 имеет объем данных V_Д = 8 бит.

В современной вычислительной технике наряду с минимальной единицей измерения данных бит широко используется укрупненная единица измерения байт, равная 8 бит. При работе с большими объемами информации для подсчета ее количества применяют более крупные единицы измерения, такие как килобайт (кбайт), мегабайт (Мбайт), гигабайт (Гбайт), терабайт (Тбайт):

1 кбайт = 1024 байт = 2¹⁰ байт;

1 Мбайт = 1024 кбайт = 2²⁰ байт = 1 048 576 байт;

1 Гбайт = 1024 Мбайт = 2³⁰ байт = 1 073 741 824 байт;.

1 Тбайт = 1024 Гбайт = 2⁴⁰ байт = 1 099 511 627 776 байт.

Количество информации I (энтропийный подход). В теории информации и кодирования принят энтропийный подход к измерению информации. Этот подход основан на том, что факт получения информации всегда связан с уменьшением разнообразия или неопределенности (энтропии) системы. Исходя из этого количество информации в сообщении определяется как мера уменьшения неопределенности состояния данной системы после получения сообщения. Как только наблюдатель выявил что-нибудь в физической системе, энтропия системы снизилась, так как для наблюдателя система стала более упорядоченной.

Таким образом, при энтропийном подходе под информацией понимается количественная величина исчезнувшей в ходе какого-либо процесса (испытания, измерения и т. д.) неопределенности. При этом в качестве меры неопределенности вводится энтропия Н, и количество информации равно:

(2.1)

где H_apr — априорная энтропия о состоянии исследуемой системы;

H_aps — апостериорная энтропия.

Апостериори — происходящее из опыта (испытания, измерения).

Априори — понятие, характеризующее знание, предшествующее опыту (испытанию), и независимое от него.

В случае, когда в ходе испытания имевшаяся неопределенность снята (получен конкретный результат, т. е. H_aps = 0), количество полученной информации совпадает с первоначальной энтропией

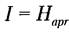
Рассмотрим в качестве исследуемой системы дискретный источник информации (источник дискретных сообщений), под которым будем понимать физическую систему, имеющую конечное множество возможных состояний. Это множество А = {a _1, a ₂,..., а_п} состояний системы в теории информации называют абстрактным алфавитом или алфавитом источника сообщений.

Отдельные состояния а₁, а₂,..., а„ называют буквами или символами алфавита.

Такая система может в каждый момент времени случайным образом принять одно из конечных множеств возможных состояний а_i.

Поскольку одни состояния выбираются источником чаще, а другие реже, то в общем случае он характеризуется ансамблем А, т. е. полной совокупностью состояний с вероятностями их появления, составляющими в сумме единицу:

, причем 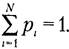(2.2)

Введем меру неопределенности выбора состояния источника. Ее можно рассматривать и как меру количества информации, получаемой при полном устранении неопределенности относительно равновероятных состояний источника.

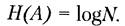(2.3)

Тогда при N = 1 получаем Н(А) = 0.

Указанная мера была предложена американским ученым Р. Хартли в 1928 г. Основание логарифма в формуле (2.3) не имеет принципиального значения и определяет только масштаб или единицу измерения В зависимости от основания логарифма применяют следующие единицы измерения.

1. Биты — при этом основание логарифма равно 2:

(2.4)

2. Ниты — при этом основание логарифма равно е:

3. Диты — при этом основание логарифма равно 10:

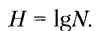
В информатике в качестве меры неопределенности обычно используют формулу (2.4). При этом единица неопределенности называется двоичной единицей, или битом, и представляет собой неопределенность выбора из двух равновероятных событий.

Формулу (2.4) можно получить эмпирически: для снятия неопределенности в ситуации из двух равновероятных событий необходим один опыт и соответственно один бит информации, при неопределенности, состоящей из четырех равновероятных событий, достаточно 2 бит информации, чтобы угадать искомый факт. Для определения карты из колоды, состоящей из 32 карт, достаточно 5 бит информации, т. е достаточно задать пять вопросов с ответами «да» или «нет», чтобы определить искомую карту.

Предложенная мера позволяет решать определенные практические задачи, когда все возможные состояния источника информации имеют одинаковую вероятность.

В общем случае степень неопределенности реализации состояния источника информации зависит не только от числа состояний, но и от вероятностей этих состояний. Если источник информации имеет, например, два возможных состояния с вероятностями 0,99 и 0,01, то неопределенность выбора у него значительно меньше, чем у источника, имеющего два равновероятных состояния, так как в этом случае результат практически предрешен (реализация состояния, вероятность которого равна 0,99).

Американский ученый К. Шеннон обобщил понятие меры неопределенности выбора H на случай, когда H зависит не только от числа состояний, но и от вероятностей этих состояний (вероятностей р_i выбора символов а_i, алфавита A). Эту меру, представляющую собой неопределенность, приходящуюся в среднем на одно состояние, называют энтропией дискретного источника информации:

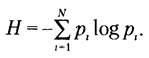(2.5)

Если снова ориентироваться на измерение неопределенности в двоичных единицах, то основание логарифма следует принять равным двум:

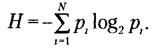(2.6)

При равновероятных выборах вероятность p_i=1/N формула (2.6) преобразуется в формулу Р. Хартли (2.3):

Предложенная мера была названа энтропией не случайно. Дело в том, что формальная структура выражения (2.5) совпадает с энтропией физической системы, определенной ранее Больцманом.

Используя формулы (2.4) и (2.6), можно определить избыточность D алфавита источника сообщений А, которая показывает, насколько рационально применяются символы данного алфавита:

(2.7)

где Н_max(А) - максимально возможная энтропия, определяемая по формуле (2.4);

Н(А) — энтропия источника, определяемая по формуле (2.6).

Суть данной меры заключается в том, что при равновероятном выборе ту же информационную нагрузку на знак можно обеспечить, используя алфавит меньшего объема, чем в случае с неравновероятным выбором.

Дата добавления: 2014-01-07