Выполнение арифметических операций с плавающей запятой

4.4.1. Смещенный код

Смещенный код, или двоичный код с избытком, используется в ЭВМ для упрощения операций над порядками чисел с плавающей запятой. Он формируется следующим образом. Сначала выби­рается длина разрядной сетки - n и записываются последовательно все возможные кодовые комбинации в обычной двоичной си­стеме счисления. Затем кодовая комбинация с единицей в старшем разряде и нулями в других разрядах (т.е. имеющая значение 2^n-1), выбираемся для представления чис­ла 0. Все последующие комбинации с единицей в старшем разряде будут представлять числа 1, 2,,3,... соответственно, а предыдущие комбинации в обратном порядке –числа -1, -2, -3,... Двоичный код с избытком для 4-разрядной сетки представлен в табл. 1.

Таблица 1

Номер кодовой комбинации	Код с избытком 8	Десятичное значение
		-1
		-2
		-3
		-4
		-5
		-6
		-7
		-8

Например, числа 3 и -3 в формате со смещением для 4-разрядной сет­ки будут иметь представление 1011 и 0101 соответственно. Нетрудно заметить, что различие между двоичным кодом с избыт­ком и двоичным дополнительным кодом состоит в противополож­ности значений знаковых битов, разность значений кодовых ком­бинаций в обычном двоичном коде и двоичном коде с избытком для 4-разрядной сетки равна 8.

В связи с этим смещенный код для 4-разрядной сетки называют двоичным кодом с избытком 8. Смещенный код можно создать для любого значения n -разрядной сетки. При этом он будет называться двоичным кодом с из­бытком 2^n-1.

Данные коды используются для упрощения операций над по­рядками чисел с плавающей запятой. Так, при размещении поряд­ка числа в 8 разрядах используется двоичный код с избытком 128. В этом случае порядок, принимающий значения в диапазоне от - 128 до +127, представляется смещенным порядком, значения ко­торого меняются от 0 до 255, что позволяет работать с порядками как с целыми без знака.

4.4.2. Представление вещественных чисел и выполнение арифметических операций над ними в ЭВМ

Десятичное число 234,47 или двоичное число 1011,01 в формате с плавающей запятой можно представить следующим образом:

231,47 = 234 470 • 10 ^-3 = 23 447 • 10 ^-2 = 2344,7 • 10 ^-1 = и т.д.

1011,01 = 101101 • 10^-10 = 1011,01 • 10⁰= 10,1101 • 10¹⁰ = 0,101101•10 ¹⁰⁰.

Такое представление чисел называется представлением с плава­ющей запятой, где порядок определяет, на сколько разрядов необ­ходимо осуществить сдвиг относительно запятой.

Если плавающая запитая расположена в мантиссе перед первой значащей цифрой, то при фиксированном количестве разрядов, отведенных под мантиссу, обеспечивается запись максимального количества значащих цифр числа, т. е. максимальная точность пред­ставления числа. Из этого следует, что мантисса должна быть пра­вильной дробью (| М| < 1), у которой первая цифра а после запя­той отлична от ноля (| М| = 0, а...). Для двоичной системы счисления а=1, поэтому |М| = 0,1... Если это требование выполнено, то число называется нормализованным. Нормализованная мантисса в дво­ичной системе счисления всегда представляется десятичным числом n, лежащим в диапазоне 0,5 < n < 1.

Примеры нормализованного представления.

Десятичная система

753,15 = 0,75315 • 10³

-0,000034 = -0,34 • 10⁴

Двоичная система

-101,01 = -0,10101• 10¹¹ (порядок 11₂ = 3₁₀);

0,000011 = 0,11 •10^-100 (порядок -100₂ = -4₁₀).

Вещественные числа в компьютерах представляются, в трех форматах — одинарном, двойном и расширенном, имеющих одинаковую структуру вида (рис. 1).

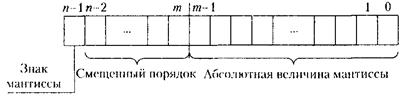
Рис. 1. Формат представления вещественных чисел

Здесь порядок n- разрядного нормализованного числа задается смещенным кодом, позволяющим производить операции над порядками как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также операцию сравнения самих нормализованных чисел.

Нормализованное число одинарной точности (32 бита), представленное в формате с плавающей запятой, записывается в память следующим образом: знак числа (знак мантиссы) — в 15 бите первого слова (0 — для положительных и 1 — для отрицательных чисел); порядок размещается в битах 7—14 первого слова, а мантисса занимает остальные 23 бита в двух словах. При этом, хотя для мантиссы отведены 23 разряда, в операциях участвуют 24 разряда, так как старший разряд мантиссы нормализованного числа не хранится (он всегда ра­вен 1), т. е. имеет место так называемый скрытый разряд, который при аппаратном выполнении операций автоматически восстанав­ливается и учитывается при выполнении операций. Порядок чис­ла также учитывает скрытый старший разряд мантиссы.

Нормализованное число двойной точности представляет собой 64-разрядное нормализованное число со знаком, 11-разрядным сме­щенным порядком и 53-разрядной мантиссой (размер поля, выде­ленного для хранения мантиссы, составляет 52 разряда, а старший бит мантиссы не хранится).

Расширенный формат позволяет хранить ненормализованные числа в виде 80-разрядного числа со знаком: 15-разрядным смешен­ным порядком и 64-разрядиой мантиссой.

Следует отметить, что вещественный формат с m -разрядной ман­тиссой дает возможность абсолютно точно представлять m -разряд­ные целые числа, т. е. любое двоичное целое число, содержащее не более m разрядов, может быть без искажений преобразовано в ве­щественный формат.

Пример. Представление чисел с плавающей запятой:

-49,5₁₀ = -110001,100₂ = - 0,1100011₂ • 10₂⁽⁶⁾₁₀, при этом порядок числа представляется двоичным кодом с избытком 128:

6₁₀ = (6 + 128)₁₀ =100 00110₂.

…

Введение термина «плавающая запятая» объясняется тем, что двоичный порядок, определяющий фактическое положение запятой в изображении числа, корректируется после выполнения каждой арифме­тической операции, т. е. запятая в изображении числа плавает (изменяет­ся ее положение) по мере изменения данной величины.

При алгебраическом сложении и вычитании чисел, представлен­иях в формате с плавающей запятой, сначала уравниваются порядки слагаемых. В процессе выравнивания порядков мантисса числа с меньшим порядком сдвигается в своем регистре вправо на количество разрядов, равное разности порядков операндов. После каждого сдвига порядок увеличивается на единицу. В результате выравнивания порядков одноименные разряды чисел оказываются расположенными в соответствующих разрядах обоих регистров, после чего мантиссы складываются или вычитаются. В случае не­обходимости полученный результат нормализуется путем сдвига мантиссы результата влево. После каждого сдвига влево порядок результата уменьшается на единицу. Ниже в примерах для упрощения расчетов порядок представлен в обычной двоичной форме.

Пример. Выполним вычитание двоичных нормализованных чисел

0,10101•10¹⁰ и 0,11101•10¹. Разность порядков уменьшаемого и вычитаемого здесь равна единице, поэтому перед вычитанием мантисса второго числа сдвигается на один разряд вправо:

0,10101 •10¹⁰

–

0,011101•10¹⁰

-----------------------

0,001101•10¹⁰

Результат получился не нормализованным, поэтому его мантисса сдвигается влево на два разряда с соответствующим уменьшением порядка на две единицы: 0,1101•10¹⁰.

При умножении порядки складываются, а мантиссы перемножаются.

Пример. Выполним умножение двоичных нормализованных чисел:

(0,11101•10¹⁰¹) • (0,1001 • 10¹¹) = (0,11101 • 0,1001) • 10^(101+11)=0,100000101 • 10¹⁰⁰⁰.

При делении из порядка делимого вычитается порядок делителя, а над мантиссами совершается обычная операция деления. В случае необходи­мости полученный результат нормализуется.

Пример. Выполним деление двоичных нормализованных чисел.

0,1111•10¹⁰⁰: 0,101•10¹¹= (0,1111: 0,101) •10^(100-11) = 1,1•10¹ =0,11•10¹⁰

Дата добавления: 2014-01-07