Ранг матрицы и его вычисление с помощью элементарных преобразований

Определение 1. Пусть задана матрица А размером m ´ n и число k £ min (m, n). Минором k -го порядка матрицы А называется определитель квадратной матрицы k -го порядка, полученной из матрицы А вычеркиванием каких-либо m - k строк и n - k столбцов.

Например, из матрицы А размером 3´4 можно получить миноры 1-го, 2-го и 3-го порядков.

Определение 2. Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы А обозначается символом rang(A) или r(A).

Ясно, что: 1) r(A) £ min (m, n);

2) r(A)=0 Û А - нулевая матрица;

3) если А - квадратная матрица n -го порядка, то r(A)=n Û ½ A ½¹0.

Определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения решения этой задачи используют преобразования, сохраняющие ранг матрицы.

Определение 3. Элементарными преобразованиями матрицы называют следующие преобразования:

1) отбрасывание нулевой строки (столбца);

2) умножение всех элементов строки (столбца) на число, не равное нулю;

3) транспонирование матрицы;

4) изменение порядка строк (столбцов) матрицы;

5) прибавление к каждому элементу строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

Теорема. Ранг матрицы при элементарных преобразованиях не изменяется.

Доказательство. Из свойств 1-4, 8 определителей следует, что при элементарных преобразованиях квадратных матриц их определители либо сохраняются, либо умножаются на число, не равное нулю. Таким образом, сохраняется наивысший порядок отличных от нуля миноров данной матрицы.

Обычно с помощью элементарных преобразований можно привести матрицу к ступенчатому виду, при котором легко определяется ранг матрицы.

Определение 4. Матрица А называется ступенчатой, если она имеет вид 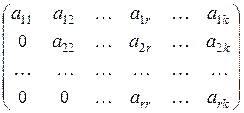, где a_ii ¹0 при i =1, 2,..., r; r £ k.

Легко получить, что ранг ступенчатой матрицы равен r.

Дата добавления: 2014-01-07