Гармонический ряд и его расходимость (доказать)

Необходимый признак сходимости рядов (доказать).

Теорема 1. (необходимое условие сходимости числового ряда). Если числовой ряд сходится, то .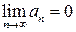

Доказательство. Ряд сходится, т.е. существует предел 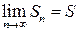. Заметим, что .

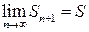Рассмотрим 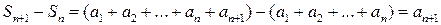. Тогда 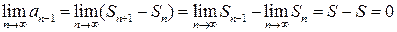. Отсюда, .

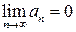Следствие 1. Если не выполнено условие 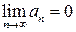, то ряд расходится.

Замечание 1. Условие 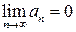не является достаточным для сходимости числового ряда . Например, гармонический ряд 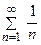расходится, хотя и имеет место .

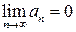Определение 1. Числовой ряд a_{n +1}+ a_{n +2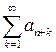}+…=, полученный из данного ряда отбрасыванием первых п членов, называется n- м остатком данного ряда и обозначается R_n.

Теорема 2. Если числовой ряд сходится, то сходится и любой его остаток. Обратно: если сходится хотя бы один остаток ряда, то сходится и сам ряд. При этом для любого n ÎN выполняется равенство S = S_n + R_n.

Следствие 2. Сходимость или расходимость числового ряда не изменится, если удалить или добавить несколько первых членов.

Следствие 3. .

32. Признаки сравнения и признак для знакоположительных рядов

Теорема 1 (признак сравнения рядов с положительными членами в неравенствах). Пусть и - ряды с неотрицательными членами, причем для каждого п ÎN выполнено условие а_n £ b_n. Тогда:

1) из сходимости ряда с большими членами следует сходимость ряда с меньшими членами;

2) из расходимости ряда с меньшими членами следует расходимость ряда с большими членами.

Замечание 1. Теорема верна, если условие а_n £ b_n выполняется с некоторого номера N Î N.

Теорема 2 (признак сравнения рядов с положительными членами в предельной форме).

Пусть и - ряды с неотрицательными членами и существует 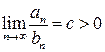. Тогда данные ряды сходятся или расходятся одновременно.

33. Признак Даламбера сходимости знакоположительных рядов

Теорема 1 (признак Даламбера). Пусть - ряд с положительными членами и существует .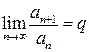

Тогда ряд сходится при q <1 и расходится при q >1.

Доказательство. Пусть q <1. Зафиксируем число р такое, что q < p < 1. По определению предела числовой последовательности, с некоторого номера N Î N выполняется неравенство a_{n +1} / a_n < p, т.е. a_{n +1}< p×a_n. Тогда a_{N +1}< p×a_N, a_{N +2}< p²×a_N. По индукции легко показать, что для любого k Î N верно неравенство, a_N+k < p^k×a_N. Но ряд сходится как геометрический ряд (p <1). Следовательно, по признаку сравнения рядов с неотрицательными членами, ряд 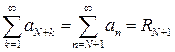также сходится. Следовательно, сходится и ряд (по теореме 2.2).

Пусть q >1. Тогда с некоторого номера N Î N верно неравенство a_{n +1}/ a_n >1, т.е. a_{n +1}> a_n. Следовательно, с номера N последовательность (a_n) является возрастающей и условие 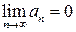не выполнено. Отсюда, по следствию 2.1, вытекает расходимость ряда при q >1.

Замечание 1. С помощью интегрального признака несложно проверить, что числовой ряд сходится, если а >1, и расходится, если a £1. Ряд называется гармоническим рядом, а ряд с произвольным a Î R называется обобщенным гармоническим рядом.

34. Знакочередующиеся ряды. Признак Лейбница сходимости знакочередующихся рядов

Исследование рядов с членами произвольных знаков представляет более трудную задачу, однако в двух случаях есть удобные признаки: для знакочередующихся рядов - теорема Лейбница; для абсолютно сходящихся рядов применим любой признак исследования рядов с неотрицательными членами.

Определение 1. Числовой ряд называется знакочередующимся, если любые два соседних члена имеют противоположные знаки, т.е. ряд имеет вид или 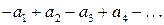, где a_n >0 для каждого n Î N.

Теорема 1 (Лейбница). Знакочередующийся ряд сходится, если:

1) (a_n) - невозрастающая последовательность;

2) при .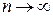

При этом модуль суммы знакочередующегося ряда не превосходит модуля его первого члена, т.е. | S |£ a ₁.

Доказательство. Пусть ряд имеет вид . Рассмотрим последовательность 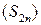. Она является неубывающей, так как для любого n Î N выполняется условие 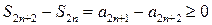, и ограниченной сверху, так как для любого n Î N выполняется условие 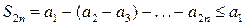. Следовательно, последовательность 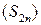сходится. Пусть 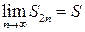. Тогда 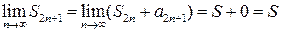. Отсюда получаем, что последовательность сходится к S, т.е. ряд сходится и имеет сумму S.

Заметим также, что , следовательно, для любого n Î N выполняется условие . Аналогичными рассуждениями доказывается, что 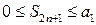, следовательно, 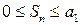. Если же ряд имеет вид 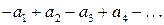, то . Следовательно, в общем случае выполняется неравенство 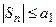. После предельного перехода при 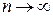получаем , что и требовалось доказать.

Следствие 1. Модуль остатка знакочередующегося ряда типа Лейбница не превосходит модуля его первого члена, т.е. .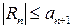

Дата добавления: 2014-01-07