
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины, их свойства
|
|
|
|
Математические операции над дискретными случайными величинами
ЛЕКЦИЯ 4
Тема 4: Дискретные случайные величины
ПЛАН
1. Математические операции над дискретными случайными величинами.
2. Математическое ожидание, дисперсия и среднее квадратическое отклонение дискретной случайной величины, их свойства.
3. Математическое ожидание и дисперсия числа m и частости m / n наступлений события в п повторных независимых испытаниях.
4. Биномиальный закон распределения и закон Пуассона.
Пусть даны две случайные величины:
| X: | xi | x 1 | x 2 | ¼ | xn | |
| pi | p 1 | p 2 | ¼ | pn |
и
| Y: | yi | y 1 | y 2 | ¼ | ym | |
| pi | p 1 | p 2 | ¼ | pm |
Произведением случайной величины Х на постоянную величину k называется случайная величина kX, которая принимает значения kxi с теми же вероятностями pi (i =1, 2, …, n).
m - ой степенью случайной величины Х называется случайная величина Xm, которая принимает значения xim с теми же вероятностями pi (i =1, 2, …, n).
Суммой случайных величин Х и Y называется случайная величина Х + Y, которая принимает все возможные значения вида xi + yj (где i =1, 2, …, n и j =1, 2, …, m) с вероятностями pij того, что случайная величина X примет значение pi, а случайная величина Y примет значение pj, т.е. pij = P [(X = xi) × (Y = yj)].
Произведением случайных величин Х и Y называется случайная величина Х × Y, которая принимает все возможные значения вида xi × yj (где i =1, 2, …, n и j =1, 2, …, m) с вероятностями pij того, что случайная величина X примет значение pi, а случайная величина Y примет значение pj, т.е. pij = P [(X = xi)×(Y = yj)].
Если случайные величины Х и Y независимы, т.е. независимы любые события X = xi и Y = yj, то по теореме умножения вероятностей для независимых событий
pij = P (X = xi)× P (Y = yj)= pi × pj.
Особое внимание следует обратить на числовые характеристики случайной величины, призванные в сжатой форме выразить наиболее существенные черты распределения, в частности, на математическое ожидание и дисперсию, и их свойства.
Определение 1. Математическим ожиданием, или средним значением, М (Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие их вероятности:
 .
.
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной:
M (C)= C.
2. Постоянный множитель можно выносить за знак математического ожидания:
M (kX)= k × M (X).
3. Математическое ожидание суммы двух случайных величин равно сумме их математических ожиданий:
M (X + Y) = M (X)+ M (Y).
4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий:
M (X × Y) = M (X)× M (Y).
5. Если все значения случайной величины увеличить на постоянную С, то математическое ожидание этой величины увеличиться на С:
M (X + С) = M (X)+ С.
6. Математическое ожидание отклонения случайной величины от ее математического ожидания равно нулю:
M (X - M (X)) = 0.
Доказательство. 2. Случайная величина kX принимает значения kxi с теми же вероятностями pi (i =1, 2, …, n), что и величина Х. Следовательно
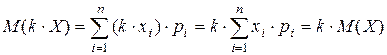 .
.
Только математическое ожидание не может в достаточной степени характеризовать случайную величину. Оно не характеризует степень отклонения принимаемых значений от среднего значения.
Определение 1. Дисперсией D (X) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания:
D (X)= M [ X - M (X)]2.
В качестве характеристики рассеяния нельзя брать математическое ожидание M (X - M (X)) отклонения случайной величины от ее математического ожидания, ибо эта величина всегда равна нулю. С другой стороны, можно было бы рассмотреть величину D (X)= M [½ X - M (X)½]. Но эта характеристика менее удобна для вычисления, чем дисперсия.
Если случайная величина Х является дискретной с конечным числом значений, то
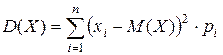 .
.
Если случайная величина Х является дискретной с бесконечным числом значений, то
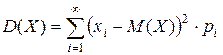 ,
,
если числовой ряд сходится.
Дисперсия D (X) имеет размерность квадрата случайной величины Х, поэтому в качестве характеристики рассеяния часто используют величину  .
.
Определение 1. Средним квадратическим отклонением s x случайной величины Х называется арифметический квадратный корень из ее дисперсии:
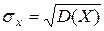 .
.
Свойства дисперсии случайной величины:
1. Дисперсия постоянной величины равна нулю:
D (C)=0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя его при этом в квадрат:
D (kX)= k 2× D (X).
3. Дисперсия случайной величины равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания:
D (X)= M (X 2) -[ M (X)]2.
4. Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий:
D (X + Y) = D (X)+ D (Y).
Доказательство. 2. Используя свойство 2 математического ожидания случайной величины X, получаем:
D (k × X) = M [ k × X - M (k × X)]2 = M [ k × X - k × M (X)]2 = k 2× M [ X - M (X)]2 = k 2× D (X).
Замечание. Числовые характеристики случайной величины Х, являясь неслучайными, постоянными, играют существенную роль в теории вероятностей. Нередко удается решить вероятностные задачи, пользуясь только числовыми характеристиками случайной величины Х, не рассматривая закон ее распределения.
3. Математическое ожидание и дисперсия числа m и частости m / n наступлений события в п повторных независимых испытаниях
Математическое ожидание и дисперсия числа т и частости 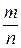 появлений события при n повторных независимых испытаниях могут быть также вычислены и по формулам:
появлений события при n повторных независимых испытаниях могут быть также вычислены и по формулам:
 . .
| (16) |
 . .
| (17) |
Теорема 1. Математическое ожидание случайной величины Х, распределенной по биномиальному закону, равно M (X)= n × p, а ее дисперсия равна D (X)= n × p × q.
Доказательство. Представим случайную величину Х как сумму n независимых случайных величин Х = Х 1+ Х 2+…+ Хk +…+ Хn, где случайная величина Хk выражает число наступлений события А в k -ом испытании (k = 1, 2, …, n) и имеет закон распределения
| X k: | xi | |||
| pi | q | p |
Вычислим математическое ожидание M (Xk) = x 1× p 1 + x 2× p 2 = 0× q +1× p = p и дисперсию
D (Xk) = (x 1- p)2× p 1 + (x 2- p)2× p 2 = (0- p)2× q + (1- p)2× p = p 2× q + q 2× p = p × q × (p+q) = p × q.
Следовательно, M (X)= M (X 1)+ M (X 2)+…+ M (Xn) = p + p +…+ p = n × p,
D (X)= D (X 1)+ D (X 2)+…+ D (Xn) = p × q + p × q +…+ p × q = n × p × q. Теорема доказана.
Следствие. Математическое ожидание частости 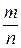 события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, равно p, то есть
события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p, равно p, то есть  , а ее дисперсия рана
, а ее дисперсия рана 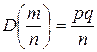 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3235; Нарушение авторских прав?; Мы поможем в написании вашей работы!