Процессы гибели и размножения

Многократно процессы перехода системы из одного рабочего состояния в другое и наоборот с так называемой деградацией можно описать с помощью процессов гибели и казни. Граф состояний переходов имеет следующий вид (рис. 2.5.).

x ₁

x_k

x_{k -1}

x_{k +1}

x ₀

m _{k +1}

m₁

m _k

…..

Рис. 2.5

Таким образом, граф состояний можно представить в виде цепи состояний, соединенных между собой стрелками переходов.

Другими словами, из любого состояния х_k (кроме крайних х¹ 0, х¹ n) возможен переход только в два соседних с ним состояния х_{k- 1} (предыдущие) и х_{k+ 1} (последующее). Из крайнего левого состояния х ₀ возможен переход только в состояние х ₁, а из крайнего правого состояния х_n только в состояние x_{n- 1}.

Такие процессы принято называть «процессами гибели и размножения». Данное название они получили потому, что впервые были применены в биологии для анализа численности популяций, распространения эпидемий и при исследовании других проблем. Так, например, если считать, что состояние х_k соответствует численности популяции, равной k, то переход системы из состояния х_k в состояние х_{k +1} происходит при рождении одного члена популяции, а переход в обратном направлении при гибели одного члена популяции. Число n может быть как конечными, так и бесконечными.

Конечное число членов популяции может иметь место в том случае, когда имеется физические ограничения на максимальную численность.

Систему дифференциальных уравнений для вероятностей состояний процесса гибели и размножения можно записать с помощью указанного выше правила:

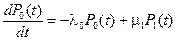; (2.86)

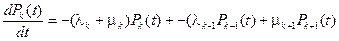; (2.87)

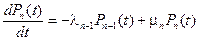, (2.88)

Эта система уравнений справедлива, как для постоянных интенсивностей потоков, так и для случая, когда интенсивности потоков являются функциями времени:

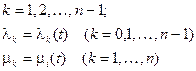. (2.89)

Для интегрирования этой системы дифференциальных уравнений нужно задать начальные условия:

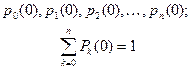(2.90)

Если число состояний n в системе конечно, то для любого момента времени выполняется условие нормирования

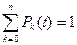(2.91)

Процессы перехода системы многократно из одного рабочего состояния в другое и наоборот с так называемой деградацией можно описать с помощью процессов гибели и казни.

Иногда рассматривается процесс размножения (чистого размножения), когда переход из состояния возможен только слева направо. Граф процесса размножения следующий (рис. 2.6).

l₀

l _{к -1}

l_к

l _{n -1}

….. ….. …..

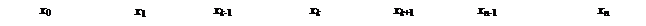Рис. 2.6

Если процесс возможен только справа налево, то такой процесс называется процессом гибели (рис. 2.7).

m₁

m _к

m _{к +1}

m _n

x_n

x_{n -1}

x_{k +1}

x_k

x_{k -1}

x ₁

x ₀

….. ….... ….

Рис. 2.7

При написании дифференциальных уравнений для вероятностей состояний процесса размножения достаточно в общей системе положить все параметры m _i =0. Аналогично для процессов гибели.

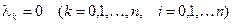(2.92)

Процесс гибели и размножения обладает эргодическим свойством, т.е. граф состояний не имеет ни одного состояния без выхода и без входа и ни одной группы состояний без выхода и без входа.

Все потоки событий, переводящие процесс из состояния в состояние, являются простейшими.

Потоки гибели и размножения называются простейшими потоками.

Контрольные вопросы

1. Дайте определение потку событий, приведите примеры.

2. Что различает потоки однородных и неоднородных событий?

3. Что представляет собой поток регулярных событий?

4. Какой поток событий будет называться потоком Пальма?

5. Дайте определение ординарному потоку событий, приведите примеры.

6. Чем характеризуется стационарный поток событий?

7. Сформулируйте определение пуассоновского потока событий, приведите примеры.

8. Опишите математическое ожидание и дисперсию интервала времени между двумя событиями (отказами и сбоями информированной системы) в простейшем потоке.

9. Какой поток событий будет регулярным?

10. Опишите нормальный поток событий.

11. Что такое поток Эрланга?

12. Дайте определение дискретному случайному процессу, приведите пример.

13. Какой случайный процесс будет марковским с непрерывным временем?

14. Чем характеризуется марковский случайный процесс с дискретным временем?

15. Составьте систему дифференциальных уравнений для вероятностей состояний.

16. Приведите доказательства взаимосвязи пуассоновского потока событий и марковского случайного процесса с непрерывным временем.

17. Опишите процесс гибели и размножения.

18. Составьте систему дифференциальных уравнений для процессов гибели и размножения.

ГЛАВА 3.

Дата добавления: 2014-01-07