Некоторые математические основы

Однородный марковский процесс. Пусть X (t) (t ³0) дискретный случайный процесс с непрерывным временем. Случайный процесс X (t) называется марковским, если для любого n= 1, 2, 3, ..., любых моментов t ₁, t ₂ ,…, t_n, t_{n+ 1}, удовлетворяющих условиям: 0 £ t ₁ £ t ₂ £…£ t_n, £ t_{n+ 1} и любых возможных значений случайного процесса i ₁, i _2,…, i_n, i_{n+ 1}выполняется следующее равенство для условных вероятностей:

. (4.18)

Марковские процессы являются математической схемой, пригодной для описания эволюции физической системы, которая в любой момент времени может находиться лишь в одном из состояний i ₁, i ₂ ,…, и для которой при заданном состоянии в данный момент времени дополнительная информация о поведении этой системы в предыдущий момент времени не влияет на условную вероятность этой системы, находиться в состоянии i_{n+ 1} в последующие моменты времени. Другими словами, процесс Маркова X (t) обладает следующим свойством: если известно X (t_n), то течение процесса после момента t_n в вероятностном смысле не зависит от его течения до момента t_n (коротко: если известно настоящее, то будущее не зависит от прошедшего).

Процесс Маркова называется однородным, если для любых возможных значений i и k и произвольного t ³ 0 вероятность события X (t _n+t) при условии X (t)= i не зависит от t. Условная вероятность называется вероятностью перехода из состояния i в состояние k за время t:

. (4.19)

Для любых состояний i и k вероятности перехода обладают свойствами:

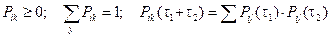. (4.20)

Последнее соотношение, называемое иногда уравнением Чэпмена-Колмогорова, лежит в основании всех исследований о процессах Маркова.

В теории надежности обычно исследуются случайные процессы двух видов: нарушений работоспособности и восстановлений работоспособности системы. Если предположить, что все распределения времени безотказной работы и времени восстановления отдельных элементов системы являются экспоненциальными, то случайный процесс X (t), характеризующий число отказов или число восстановлений, является однородным марковским процессом.

Инженерные расчеты показателей надежности ММП без привлечения ЭВМ могут быть выполнены лишь для сравнительно небольших структур системы; такие структуры называются типовыми. Для систем с большим числом состояний появляются вычислительные трудности, связанные, с решением систем дифференциальных или алгебраических уравнений высокого порядка.

Преобразование Лапласа лежит в основе операционного метода решения линейных дифференциальных уравнений и систем. Оно позволяет преобразовать любую систему линейных дифференциальных уравнений в систему линейных алгебраических уравнений.

Пусть функция f (t) кусочно-непрерывна при t ³0 и имеет ограниченный рост, т.е. ê f (t)½£ Се ^{a ,t,}, где С и a - некоторые постоянные. Тогда она называется оригиналом, а функция – ее изображением.

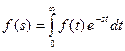. (4.21)

Для обозначения оригинала и изображения можно пользоваться одним и тем же символом. Переход от оригинала к изображению называется преобразованием Лапласа, а переход от изображения к соответствующему оригиналу – обратным преобразованием Лапласа:

- если f (t)= c ₁ f ₁(t)+ c ₂ f ₂(t), то f (s)= c ₁ f ₁(s)+ c ₂ f ₂(s), где c ₁ и c ₂ – любые постоянные числа;

- изображением производной f¢ (t) является функция sf (s)- f (t)ê _{t =0}.

При вычислении финальных (предельных) значений функций можно использовать следующее равенство:

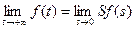. (4.22.)

Решением системы алгебраических уравнений является набор дробно-рациональных функций вида:

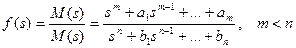. (4.23)

Если знаменатель дроби N (s) имеет только простые корни s ₁, s ₂, … s_n, то f (t) функции f (s) определяется равенством

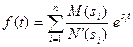. (4.24)

Если знаменатель дроби N (s) имеет кратные корни: s ₁ - кратности r ₁, s ₂ – кратности r ₂, s_k – кратности r_k (r ₁ + r ₂+ …+ r_k = n), то оригинал f (t) функции f (s) определяется равенством

, (4.25)

где коэффициенты А_ij находят по формуле:

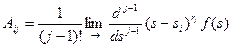. (4.26)

i =1, 2, …, k j =1, 2, …, r

Дата добавления: 2014-01-07