Градиент скалярного поля

Определение. Градиентом скалярного поля 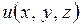в точке 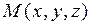называется вектор, обозначаемый .

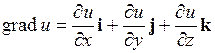Вектор 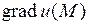указывает направление наискорейшего возрастания функции 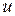в точке 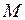стороны, 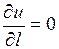, вектор 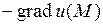указывает на направление наискорейшего убывания функции 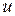в точке .

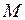Векторное поле и его характеристики: векторные линии, поток поля через поверхность

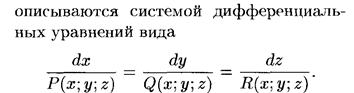
Поток векторного поля

Рассмотрим физический смысл потока векторного поля (поверхностного интеграла второго рода). Пусть в некоторой области 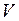евклидова пространства 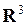течет со скоростью 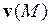жидкость, имеющая объемную плотностью 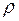. Вычислим количество жидкости протекающей через некоторую гладкую поверхность 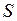, расположенную в области 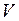. Для этого ориентируем 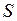единичным вектором нормали 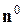и разобьем поверхность на части 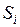, 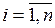столь малого диаметра, чтобы они практически не отличались от своих плоских площадок. Пусть 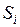одна из таких частей с единичным вектором нормали 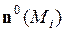. Тогда через 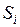в направлении нормали 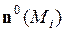протечет в единицу времени 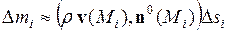жидкости, где 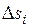– площадь части 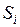. Это выражение для количества 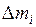жидкости будет тем точнее, чем меньше диаметр 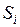. Заметим, что 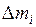будет положительным, если жидкость течет через 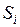в направлении вектора 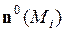и отрицательным – в противоположном случае. Общее количество 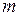жидкости, протекающей через поверхность 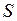, приблизительно равно

.

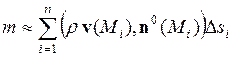Переходя к пределу в этом выражении при 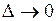, где 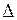– максимальный диаметр частей 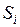, , 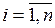находим

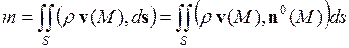. (4.3.10)

Формула (4.3.10) определяет поток (количество) жидкости через выбранную сторону поверхности 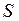, заданную вектором 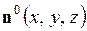, и физический смысл поверхностного интеграла второго рода.

Если 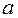– поле сил, то говорят, что поток векторного поля

,

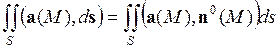равен количеству силовых (векторных) линий, пронизывающих в единицу времени поверхность 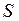в направлении .

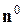Дата добавления: 2014-01-07