Комплексный чертеж плоскости

Плоскость есть такое множество точек, основные свойства которого выражаются следующими аксиомами:
Через три точки, не принадлежащие одной прямой, проходит одна и только одна плоскость. Следствия:

через прямую и не принадлежащую ей точку можно провести одну и только одну плоскость;

через две пересекающиеся прямые можно провести одну и только одну плоскость;

через две различные параллельные прямые можно провести только одну плоскость.

Прямая, проходящая через любые две различные точки плоскости, принадлежит этой плоcкости (если две точки прямой принадлежат плоскости, то и все точки этой прямой принадлежат плоскости).

Если две различные плоскости имеют общую точку, то их пересечение есть прямая (две плоскости пересекаются по прямой линии).

Плоскость может занимать различные положения относительно плоскостей проекций. Плоскость, не параллельная и не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Задать плоскость на чертеже проекциями множества ее точек практически невозможно, т. к. проекции точек плоскости покроют плоскости проекций и мы не получим на них никаких изображений. Поэтому плоскость на чертеже задают проекциями таких принадлежащих ей геометрических фигур, которые однозначно определяют ее положение в пространстве и позволяют построить любую ее точку.
На основании аксиомы 1 и следствий из нее плоскость общего положения на чертеже можно задать (рис. 2.3. а, б, в, г, д):

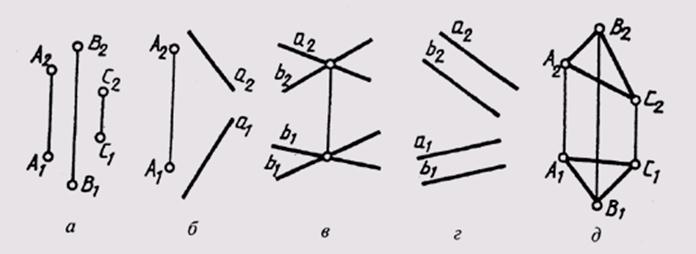
Рис 2.3

а) проекциями трех точек, не принадлежащих одной прямой линии;
б) проекциями прямой и не принадлежащей ей точки;
в) проекциями двух пересекающихся прямых;
г) проекциями двух различных параллельных прямых;
д) проекциями плоской фигуры.

Плоскость, не перпендикулярная ни одной из плоскостей проекций, называется плоскостью общего положения. Плоскость, перпендикулярная хотя бы одной из плоскостей проекций, называется плоскостью частного положения.

Дата добавления: 2014-01-07