Ошибки выборки

Расхождение между характеристиками выборки и генеральной совокупности составляет ошибку выборки. Она зависит от вариации изучаемого признака, численности выборки, методов отбора единиц в выборку, принятого уровня достоверности результата.

Количество отобранных в выборочную совокупность единиц определяют исходя из принятой доли выборки К_В

К_В =Доля выборки = = .

Например, при К_В = 5% выборки из партии N = 1000 единиц объем выборки n = 50 единиц, а при К_В = 10% – n = 100 единиц.

Различают два вида обобщающих показателей:

· относительную величину альтернативного признака, т.е. долю р (удельный вес)единиц совокупности, обладающих данным значением признака (например, доля нестандартных изделий в партии товара, удельный вес продукции собственного производства в товарообороте общепита, удельный вес продавцов в общей численности);

· среднюю величину количественного признака.

Выборочная доля ( ), или частость, определяется отношением числа единиц m, обладающих изучаемым признаком, к общему числу выборочной совокупности n.

Например, если из 100 деталей (n = 100) 95 оказались стандартными (m = 95), то выборочная доля .

Для характеристики выборочных показателей используют понятие ошибки выборки.

При случайном повторном отборе средние ошибки рассчитываются по формулам:

· для среднего количественного признака ,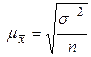

· для доли (альтернативного признака) .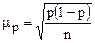

Так как 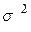, дисперсия признака в генеральной совокупности точно неизвестна, на практике пользуются значением дисперсии , рассчитанным для выборочной совокупности на основании закона больших чисел (выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики генеральной совокупности). Генеральная дисперсия выражается через выборочную . При достаточно больших n можно принять . Среднее и дисперсия количественного признака в выборке определяется по формулам

.

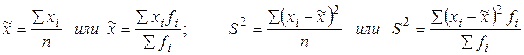Тогда формулы средних ошибок примут вид

При случайном бесповторном отборе численность генеральной совокупности в ходе выборки сокращается. Формулы для среднего значения количественного признака и для доли имеют вид:

, .

Малые выборки. Под малой выборкой понимается несплошное статистическое обследование с небольшим числом единиц – от 4 до 30. Тогда:

1. Генеральная дисперсия выражается через выборочную по формуле: .

2. Средняя ошибка малой выборки при повторном отборе имеет вид: .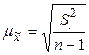

Распространение выборочных результатов на генеральную совокупность производится с учетом закона больших чисел, который определяет с заданной вероятностью предел возможной ошибки различий средних. Для выборок при n>30 значения t и Ф(t) приведены в таблице.

T		1.960		2.58
Ф(t)	0.683	0.95	0.954	0.99	0.997

Таким образом при заданной вероятности Ф(t) и определяемом из таблицы значении t можно определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:

· для средней величины количественного признака ,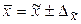

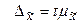
для доли альтернативного признака ,

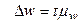
Например, при Р = 0,683 ® t = 1. Следовательно в 68,3% случаев ошибка не выйдет за пределы 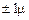(одной средней ошибки выборки).

Распространение характеристик выборки на генеральную совокупность производится следующими способами.

Способ прямого расчета состоит в том, что показатели выборочной доли w, или средней 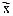распространяются на генеральную совокупность с учетом ошибки выборки (количество поступивших в партии товаров нестандартных изделий, …).

Способ поправочных коэффициентов применяется в случаях, когда целью выборочного метода является уточнение результатов сплошного учета (ежегодная перепись скота у населения, …). Для этого после обобщения данных сплошного учета практикуется 10% выборочное обследование с определением так называемого «процента недоучета».

Дата добавления: 2014-01-07