Нечёткие системы управления

Связь с теорией вероятностей.

Математическая часть.

Нечёткое (или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. Л. Заде расширил классическое канторовское понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1.

Теория нечётких множеств в определенном смысле сводится к теории случайных множеств и тем самым к теории вероятностей. Основная идея состоит в том, что значение функции принадлежности можно рассматривать как вероятность накрытия элемента некоторым случайным множеством.

Однако при практическом применении аппарат теории нечётких множеств обычно используется самостоятельно, выступая конкурентом к аппарату теории вероятностей и прикладной статистики.

В настоящее время начинают находить широкое применение так называемые нечеткие системы управления (fuzzy-системы), основанные на нечеткой логике и использующие теорию нечётких множеств. Особенно эффективно применение нечетких систем управления там, где объект управления достаточно сложен для его точного описания и существует дефицит априорной информации о поведении системы. Область применения нечетких систем управления показана на рис.1.

Рис. 1. Сфера применения нечетких систем управления.

Принцип действия нечетких систем управления основан на выполнении нечеткого логического вывода типа < Если А, то Б >. Нечеткие системы имеют базу знаний и зачатки искусственного интеллекта.

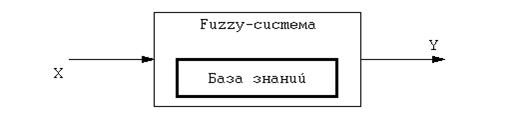
Рис.2. Простейшая одновходовая нечеткая система.

Простейшая система управления, функциональная схема которой показана на рис. 2, реализует один восходящий нечеткий вывод, схему которого можно представить в следующем виде

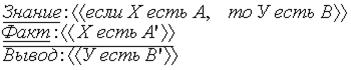
Здесь 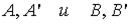- описательная информация - лингвистические переменные, представляемые в виде нечетких множеств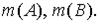

Недостатками нечетких систем являются:

· отсутствие стандартной методики конструирования нечетких систем;

· невозможность математического анализа нечетких систем существующими методами;

· применение нечеткого подхода по сравнению с вероятностным не приводит к повышению точности вычислений.

Дата добавления: 2014-01-07