Диалектическая целостность

Пример

Ригидность

Управление в произвольных ситуациях

Диалектика требует рассмотрения явления в его возможном дальнейшем развитии в будущем.

Казанцев является бакалавром () и учится (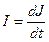) на магистра. Характеризуя его, надо оценить его намерение 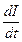продолжить или прекратить своё образование, т.е. оценить вероятность того, что он не прекратит своё обучение в ближайшем будущем.

Способность человека сохранять верность своим целям, т.е. способность эволюционировать с постоянной скоростью, несмотря на возникающие помехи, именуют ригидностью.

Это качество неоднозначно: его роль положительна, если рассматривать борьбу с помехами, и отрицательна, если она препятствует быстрой перестройки для достижения сменившихся целей.

Поэтому в применении к человеку ригидность называют в первом случае стойкостью и целеустремлённостью, а во втором – косностью и догматизмом.

Но мы применяем эту характеристику инерционности не только к людям, поэтому будем называть это явление нейтральными терминами «ригидность» и «индуктивность», трактуя их как синонимы и обозначая L.

Вернёмся к примеру с идентификацией русских букв.

Предельный темп 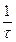, где 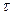- среднее время опознания буквы, может быть достигнут по мере выработки навыков.

Темп опознания (различения) будет постоянно возрастать от 0 до .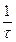

Пусть выработка навыков происходит с постоянной скоростью и занимает время . Тогда предельное для данного индивида ускорение темпа распознавания букв составит: , а величина, обратная этому предельному ускорению и есть индуктивность L, которая имеет размерность квадрата времени 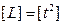. 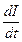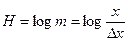Более точно , поскольку в линейных системах вероятность p того, что реальное ускорение процесса меньше предельного, подчиняется закону , а с учётом выражения получим:

. (24)

Любое уравнение применительно к логике– это суждения

Соотношение (24) относится к суждениям типа «Способность Казанцева проявлять настойчивость (волю) 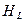в условиях помех 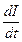составляет ».

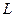Применительно к техническим системам выражение (24) характеризует инерционность механического или электрического происхождения, а применительно к человеку – его волевые качества, так что 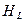есть логарифм вероятности того, что целенаправленная система сохранит движение к цели, а человек преодолеет препятствия на своём пути.

В выражении (24) представлено суждение лишь о намерениях, желаниях, воле к чему-либо без непременной актуализации этих намерений. Но сочетание выражений (24) и (19) констатирует не только намерения, но и движение к цели:

, (25)

а с учётом выражения (13) это будет исчерпывающее суждение, присущее диалектической логике:

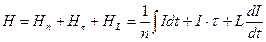, (26)

Эта форма присуща, например, резюме, которое пишет лицо, претендующее на занятие должности (H_n – биографические данные, H_τ – исполняемая в данный момент работа,
H_L – способность выполнять будущую работу.)

Это суждение H= ∫Idt+Iτ + L 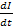позволяет делать ряд умозаключений на основе изучения и решения этого дифференциального уравнения, т.е. оно (суждение) сводит формализм диалектической логики к математическим операциям.

Например, известно, что динамическая система, описываемая линейным дифференциальным уравнением второго порядка, склонна к колебаниям информационного тока, т.е. к колебаниям в своем движении к цели, в тем большей степени, чем меньше τ и n и чем больше L. Если L=0
(H = + Iτ) при внезапном исчезновении непосредственного стимула система начинает отрабатывать назад, т. е. удаляться от цели стимулирования. При L=0 и n=0 система постепенно перестает двигаться к цели, но не возвращается к исходному состоянию. При n=∞ и τ=0 система самостоятельно продолжает работу в том же темпе, в каком его застало исчезновение стимула и т.д. Все эти умозаключения делаются посредством математического аппарата и демонстрируют тот факт, что математика по существу представляет собой достаточную основу для автоматизации весьма сложного поведения.

Системная суть:
H_с=H_в+H (H_с - системная суть, H_в - взаимная суть, H - собственная суть. )

Так же представим и системную индуктивную сущность:
H_Lс=H+H_в=L 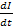+L_в , где
I - собственный информационный ток элемента системы,
- приведенный информационный ток всех других элементов системы, индуктивно связанных с рассматриваемым элементом (действия, которые субъект производит «заодно»с объектом.)
L характеризует собственные качества элемента системы(например, человека), рассматриваемого вне связи с другими элементами,
L_в характеризует такие качества элемента, как способность к совместной работе (совместимость) с другими элементами, уживчивость, способность считаться с чужим мнением или поведением (или противостоять им). L_в относится к суждениям типа «Подходящий (неподходящий) элемент».

В общем случае: n, τ и L=f(информационный токI), поэтому система уравнений:
H_i= 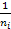∫I_idt+I_iτ+ L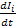_i ǀ, _i=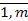
представляет собой универсальную диалектическую модель бытия, пригодную для исчерпывающего описания логики системы с сосредоточенными параметрами любого происхождения и структуры, исследование которой исчерпывается формальным математическим аппаратом. Например, логика экономической системы с позиций информационного подхода должна описываться системой развернутых уравнений типа (26) в виде:

H₁= 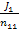+ … + +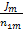I₁τ₁₁+ … + I_mτ_1m+L₁₁ + … + L_1m ;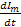
................................................
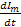H_m= + … + + I₁τ_m1+ … + I_mτ_mm +L_m1 + … + L_mm , где

H_kǀk= 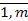– относительная цена (в битах) единицы продукта J_k = ∫I_kdt;
I_k –выпуск в битах (т.е. в штуках) продукта J_k в единицу времени;
n_ik –емкость рынка для i-го продукта при наличии k-го продукта;
τ_ik – время производства одной штуки i-го продукта при условии параллельного выпуска k-го продукта и при максимальной производительности труда;
L_ik –взаимозаменяемость (взаимообусловленность) i-го и k-го продуктов;
L_kk –влияние привычек (инерции) потребителей на сбыт k-го продукта.

Решение такой системы позволяет грамотно спланировать динамику выпуска продукции
I_k= f_k(t) для любой предписанной программы изменения цен H_k= φ_k(t), а ее анализ позволяет определить устойчивость экономики, совместность и избыточность тех или иных продуктов и др.

На основании изложенного можно говорить о динамической целостности системы: α( 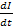), определяемой влиянием ускорения (замедления) 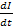эволюции каждой из ее частей на эволюцию системы как целого. Взаимная суть системы может определяться как взаимной индуктивностью частей, так и схемным (топологическим) взаимодействием их собственных индуктивностей.
Динамическая целостность всегда определяется соотношением:
α( ) = – .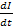
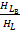Вернемся к примеру с журнальными статьями: если пропускная способность журнала выросла за год от 90 до 100 статей в год, а пропускные способности отдельных тематик изменились за то же время соответственно:
30 → 40; 25 → 30; 18 → 20; 17 → 10 статей в год, то согласно
H_L=L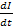
индуктивности (ригидности) журнала и отдельных тематик составят:
L_c= 0,1 год²; L₁= 0,1 год²; L₂= 0,2год²; L₃= 0,5 год²; L₄= - 0,143год².

Если при этом поток статей, поступающих в журнал, изменился за год от 150 до 200 статей/год, а по отдельным тематикам соответственно:
(1) 35 → 50; (2) 35 → 50; (3) 40 → 50; (4) 40 → 50 статей/год, то согласно
H_L=L 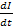будет:
H_с = 0,1×50 = 5 бит,
H₁= 1,5 бит; H₂= 3 бит; H₃ = 5 бит; H₄ = - 1,43 бит.

Поскольку на каждую из тематик априорно приходится по 0,25×H_с = 1,25 бит, то согласно формуле α( 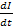) = –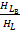, динамическая целостность отдельных тематик составит:
α₁ = = 0,167; α₂ = 0,583; α₃ =0,75; α₄ = 1,87,
а целостность всего журнала α( 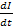) = 0,368.

Все рассмотренные частные оценки включаются в диалектическую целостность системы. Она полностью и всесторонне характеризует переход количества частей в новое качество целого:
α(J, I, 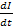) = – = 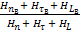= 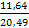0,568, где
H_n=– = ;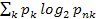
H_τ=– 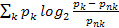=Iτ;
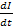H_L=– =L , где
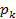– вероятность k –го состояния с учетом динамики системы;
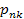– вероятность того же состояния в установившемся режиме, в статике.

Из этих выражений следует, что сущность системы в статике (H_n) всегда положительна, а статическая целостность ≤ 1. С другой стороны, кинетическая (H_τ) и динамическая (H_L) сущности могут быть как <0, так и >0, а соответствующие оценки целостности могут быть как <1, так и >1.

Система любой природы тем совершеннее и устойчивее, чем больше ее целостность. Отрицательно целостные (парадоксальные) системы неустойчивы и тяготеют к распаду. Ускоренно развивающиеся системы потенциально обладают большей целостностью и устойчивостью, нежели системы, застывшие в своем развитии.

Дата добавления: 2014-01-07