Пример 5.3.4

Goal

Clauses

Predicates

Domains

s =symbol

l= s*

preemn (s, l)

gs(s)

solve (l, l, l)

sol

sol:- solve ([S], P), write(“Sol=”,P), nl.

solve(V, [V]):- gs(V).

solve(V,[V|P]):- preemn (V, [V1|N]), solve(V1, P).

solve(V, P):- preemn(V,[]), P=resh.net,write(P),nl.

sol.

Программа представляет собой реализацию стратегии поиска в глу­бину на корневом дереве. Ее называют поиском в глубину потому, что программа ведет поиск, выбирая самую глубокую вершину для построения пути - ту, которая расположена дальше всех от начальной вершины. На рис. 5.10.показано, в каком порядке посещаются узлы. Этот порядок соот­ветствует трассировке выполнения программы при поиске цели sol.

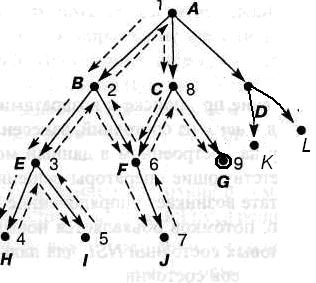
Рис.5.9. Схема поиска с возвратами

Рис.5.10. Схема поиска в глубину.

Поиск в глубину в наибольшей степени приемлем для рекурсивного стиля про­граммирования на языке Турбо- Пролог так как сама система при выполнении цели проверяет варианты по принципу поиска в глубину.

Поиск в глубину может привести к процессу, разворачивающемуся вдоль некоторого бесполезного пути, поэтому нужно ввести некоторую процедуру возвращения: после того как в ходе процесса строится вершина с глубиной, превышающей некоторую граничную глубину, раскрывается вершину наибольшей глубины, не превышающей этой границы, и т.д. При этом возникает оп­ределенное затруднение, связанное с тем, что подходящий предел необходимо уста­навливать заранее. Если этот предел будет установлен слишком низким (т.е. мень­шим по сравнению с длиной любого пути решения), поиск завершится неудачей. А если предел будет установлен слишком высоким, поиск потребует лишних затрат времени. Для преодоления этой сложности можно выполнять поиск в глубину итера­тивно, постепенно изменяя предел глубины, начиная с очень низкого предела глуби­ны и постепенно увеличивая этот предел до тех пор, пока не будет найдено решение. Этот метод называется итеративным углублением. Его можно реализовать путем модификации программы примера 5.3.2, введя параметр максимальной глубины.

/*Программа: поиск в глубину */

Дата добавления: 2014-01-07