Цветовой треугольник МКО

Колориметрическая система МКО

Первая стандартная колориметрическая система (RGB) принята в 1931 г. на VIII сессии МКО (Международная комиссия по освещению). В качестве трех линейно независимых цветов были выбраны монохроматические излучения: красный R (700 нм), зеленый G (546,1 нм), и синий B (435,8 нм). Красный цвет был получен с помощью красного светофильтра из спектра лампы накаливания, зеленый и синий выделены из спектра ртутной лампы высокого давления. Одновременно была принята еще одна система: XYZ, в которой в качестве основных независимых цветов были приняты нереальные цвета, чтобы избежать отрицательных координат. Но об этой системе поговорим позже.

В основе измерения цвета лежат три закона аддитивного синтеза цвета - законы Грассмана:

1. Любой цвет однозначно выражается через три цвета, если они линейно независимы. Последнее означает, что никакой из этих трех цветов не может быть выражен через два других. Этот закон утверждает трехмерность феномена цвета.

2. При непрерывном изменении излучения цвет смеси также меняется непрерывно. Нет такого цвета, к которому нельзя было бы подобрать бесконечно близкий цвет.

3. Закон аддитивности цветовых уравнений: если цвета смешиваемых излучений описываются цветовыми уравнениями, то цвет смеси выражается суммой цветовых уравнений.

Из первого закона Грассмана следует, что любой цвет можно представить вектором в трехмерном пространстве, где независимые цвета будут расположены вдоль трех выбранных осей координат. Практически это означает, что для измерения любого цвета необходимо каким-либо образом уравнять измеряемый цвет с цветом сравнения, образованным тремя световыми потоками, взятыми в нужной пропорции. Например, первый цвет направляется на одну грань гипсовой призмы, а три световых потока - на другую. Потоки регулируют до тех пор, пока цвета визуально не будут казаться совершенно одинаковыми. Приборы, основанные на подобном уравнивании, называются калориметрами. В данном случае конкретное их устройство не имеет значения.

В системе RGB три взаимно перпендикулярных оси соответствуют трем векторам RGB. Тогда любой цвет Ц можно выразить в виде цветового уравнения:

Ц = R R + G G + B B,

где R,G и B - цветовые координаты. Цветовые координаты показывают, сколько единиц каждого из трех основных цветов нужно взять, чтобы получить данный цвет Ц. Цвет Ц изображается цветовым векторомЦ, проведенным из начала координат в точку цвета Ц. Длина вектора цвета выражает яркость и зависит от цветовых координат. Масштабы вдоль трех осей выбирают так, чтобы при равенстве цветовых координат получился белый цвет (точка Б): R=G=B. При нулевых цветовых координатах - цвет черный (точка Ч): R=G=B= 0. Линия, соединяющая точки Ч и Б является ахроматической осью, на ней располагаются все возможные ахроматические цвета от черного до белого. По мере удаления от ахроматической оси насыщенность цвета увеличивается. В направлении (от Ч до Б), параллельном этой оси, увеличивается светлота, т.е. доля белого в цвете. Собственно, описанное трехмерное представление системы цветов представляет собой цветовое тело МКО 1931 года.

Опыт показывает, что для многих цветов цветовое уравнение выполняется, если допустить, что некоторые цветовые координаты могут быть отрицательными. Это соответствует тому, что в эксперименте по уравниванию полей при измерении цвета какой-то поток нужно добавить не в сумму цветов, а к измеряемому цвету, например:

Ц + G G = R R + B B, Þ Ц = R R - G G + B B (13.1)

Если на осях отложить выбранные векторы R, G и B, и соединить их концы, то получится цветовой треугольник, который называется треугольником цветности. В вершинах треугольника по условиям построения находятся точки основных цветов. Тогда положение точки любого цвета будет изображаться проекцией некоторой точки в плоскости треугольника, и для задания этого цвета достаточно двух координат. Точка белого цвета находится на пересечении высот треугольника.

Единицы, в которых измеряются цветовые потоки R, G и B могут быть по-разному нормированы. Например, в системах отображения цвета компьютерными мониторами, принято выражать цветовые координаты числами от 0 до 255. В других системах в тех же пределах задаются значения светлоты, чистоты (насыщенности) цвета, а также яркости. Причины - скорее исторические, но и по ступеням различения всех указанных величин такая растяжка даже с некоторым запасом перекрывает возможности человеческого глаза. В колориметрии вводятся свои единицы. Нет смысла выбирать одинаковые единицы для всех задач, потому что человеческий глаз обладает очень большим диапазоном различения потоков излучения по их интенсивности (различающимся в 10¹² раз!). Поэтому есть смысл сначала определиться с задачей измерения, а затем уточнить подходящие единицы измерения цветовых потоков.

На практике часто используют относительные величины. Относительные значения координат цвета называются координатами цветности и обозначаются буквами r, g, b:

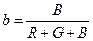; ; . (13.2)

Очевидно, сумма координат цветности равна единице:

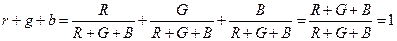. (13.3)

Или

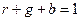. (13.4)

Координаты цветности связаны этим условием и поэтому независимыми могут быть только две из них, например, если r и b заданы, то g необходимо равно

.

В этом случае также можно построить треугольник, в котором можно упорядочить цвета. Чтобы понять, как это выполняется, вспомним теорему из геометрии: если опустить на три стороны равностороннего треугольника из любой точки три перпендикуляра, то их алгебраическая сумма будет равна высоте треугольника. Если точка лежит вне треугольника, то длины некоторых перпендикуляров будут отрицательными. Выберем высоту, равную единице. Поскольку это равноценно условию (13.1), то можно условиться каждый цвет изображать той точкой в треугольнике или вне него, у которой координаты цветности равны длинам соответствующих перпендикуляров. Потоки основных цветов RGB выбраны так, чтобы их сумма давала белый свет. Основные цвета RGB поместим в вершины треугольника, тогда их координаты цветности соответственно равны R (1,0,0); G(0,1,0); B(0,0,1). Для других цветов, соответствие определяется так. Например, если перпендикуляр опущен на сторону, лежащую против вершины В, то его длина равна цветовой координате в; если перпендикуляр опущен на сторону, лежащую против вершины G, то его длина равна цветовой координате g (рис.13.1, а). Точка белого цвета (Е) находится на пересечении высот, которые в равностороннем треугольнике совпадают с медианами, следовательно, точка белого цвета имеет координаты цветности, равные 1/3: Ц (1/3, 1/3, 1/3). (Если кто не помнит, точка пересечения медиан делит каждую из них в отношении 1:2).

Рис.13.1, б) показывает, как появляются отрицательные координаты цветности. Внутри цветового треугольника лежат все цвета (так мы в дальнейшем будем для краткости выражать мысль: все точки, изображающие цвета в цветовом треугольнике), которые могут быть получены смешиванием трех цветовых потоков RGB. Вне цветового треугольника лежат цвета, которые не могут быть получены непосредственно смешиванием трех цветовых потоков RGB.

Цвета, расположенные на сторонах цветового треугольника, могут быть получены смешиванием двух основных цветов, которые находятся в вершинах, которые этой стороной соединяются. Таким образом, на сторонах цветового треугольника располагаются цвета, получающиеся в результате смешения основных цветов попарно. На каждой биссектрисе располагаются цвета, получающиеся при смешении каждого из основных цветов с белым цветом Е, расположенным в центре.

Дата добавления: 2014-01-07