Разветвленные цепи. Правила Кирхгофа

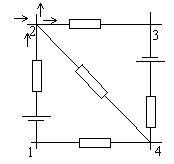Электрическая цепь, содержащая в себе узлы, называется разветвленной. Узел – место в цепи, где сходятся три или более проводников (рис.5.14). Для расчета разветвленных цепей применяют правила Кирхгофа (Kirchhoff G.,1824-1887), являющиеся прямым следствием основных законов теории электричества. Этих правил два.

Рис.5.14. Участок разветвленной цепи.

Первое правило: алгебраическая сумма всех токов, сходящихся в узле равна нулю:

Первое правило Кирхгофа является следствием закона сохранения заряда в применении к узлу, через который протекают постоянные токи. Если в цепи имеется N узлов, то пишется N -1 уравнение для любых узлов.

Второе правило: для любого замкнутого контура, выделенного внутри разветвленной цепи, алгебраическая сумма падений напряжений на сопротивлениях равна алгебраической сумме ЭДС, действующих в этом контуре:

Второе правило Кирхгофа является следствием равенства нулю циркуляции электро- статического поля по замкнутому контуру, то есть следствием его потенциальности.

. 2.7. Соединение сопротивлений.

Соединение сопротивлений бывает последовательным, параллельным и смешанным.

1) Последовательное соединение.

При последовательном соединении ток, текущий через все сопротивления, одинаковый, а падения напряжения разные (рис.5.15).

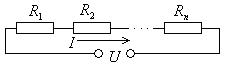
Рис.5.15. Последовательное соединение сопротивлений.

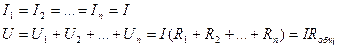, откуда следует, что

2) Параллельное соединение.

При параллельном соединении падения напряжения на всех сопротивлениях одинаковые, а токи, текущие в них, разные (рис.5.16).

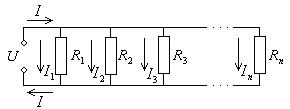
Рис.5.16. Параллельное соединение сопротивлений.

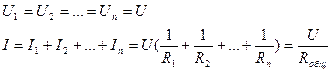, откуда следует, что

2.8. Работа и мощность постоянного тока. Закон Джоуля – Ленца.

.При протекании по проводнику электрического тока проводник нагревается. Нагревание происходит за счет работы, совершаемой силами поля над носителями заряда:

,

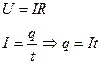
Рис.5.17. Проводник с током.

Джоуль (Joule J., 1818-1889) и независимо от него Э.Х.Ленц (1804-1865) установили экспериментально, что количество теплоты, выделяющейся в проводнике, пропорционально квадрату силы тока, сопротивлению проводника и времени протекания тока:

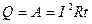
Если сила тока изменяется со временем, то за промежуток времени Δt = t₂ – t₁ выделится теплота:

Написанные соотношения выражают собой закон Джоуля – Ленца.

Если теплоту измерять в калориях, то: .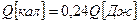

Количество теплоты, выделяющееся в единице объема проводника за единицу времени, называется удельной мощностью:

, где 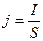- плотность тока.

Это соотношение представляет собой закон Джоуля-Ленцавдифференциальной форме:

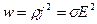
Работа, производимая током за единицу времени, называется мощностью:

.

Размерность мощности в СИ: (ватт).

Дата добавления: 2014-01-07