Движение заряженной частицы в однородном постоянном магнитном поле

В данном случае 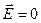и сила Лоренца имеет только магнитную составляющую 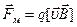. Уравнением движения частицы, записанном в декартовой системе координат, в этом случае является:

.

Рассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля (рис.13.3).

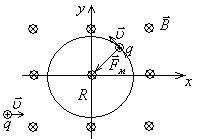
Рис.13.3. Движение заряженной частицы в магнитном поле ().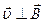

В системе координат, показанной на рис.13.3, 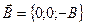, , и уравнение движения принимает вид:

,

откуда следует, что вектор полного ускорения частицы лежит в плоскости, перпендикулярной вектору 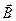. Легко убедиться также в том, что вектор ускорения перпендикулярен вектору скорости частицы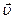и составляет вместе с вектором 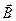правую тройку векторов (как и должно быть по свойствам силы Лоренца). Действительно,

.

Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен:

.

Траекторией движения является окружность, радиус R которой находим из условия: , то есть 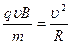, откуда:

.

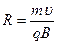Период обращения частицы

Отметим, что период обращения и соответственно угловая скорость движения частицы 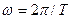не зависят от линейной скорости .

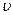Рассмотрим теперь случай, когда частица влетает под углом α к силовым линиям магнитного поля (рис.13.4).

Рис.13.4. Общий случай движения заряженной частицы в однородном магнитном поле.

Разложим вектор скорости 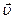на две составляющие: - параллельную вектору 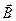и - перпендикулярную 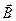. Поскольку составляющая силы Лоренца в направлении 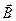равна нулю, она не может повлиять на величину . Что касается составляющей , то этот случай был рассмотрен выше. Таким образом, движение частицы можно представить как наложение двух движений: одного – равномерного перемещения вдоль направления силовых линий поля со скоростью , второго – равномерного вращения в плоскости, перпендикулярной 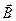. В итоге траекторией движения будет винтовая линия (рис.13.4).

Шаг винтовой линии определяется по формуле:

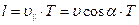, где .

Радиус витка находим по формуле:

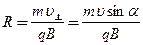
Направление, в котором закручивается винтовая линия, зависит от знака заряда частицы. Если заряд частицы положительный, то винтовая линия закручивается против часовой стрелки, если смотреть вдоль направления 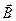, и наоборот – по часовой стрелке, если заряд частицы отрицательный.

Дата добавления: 2014-01-07