Свободные затухающие колебания. Добротность колебательного контура

Всякий реальный колебательный контур обладает сопротивлением (рис.16.3). Энергия электрических колебаний в таком контуре постепенно расходуется на нагревание сопротивления, переходя в джоулево тепло, вследствие чего колебания затухают.

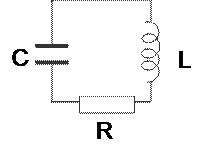
Рис.16.3. Колебательный RLC-контур.

Уравнение свободных затухающих колебаний можно получить, исходя из того, что в отсутствии внешнего источника напряжения, сумма падений напряжений на индуктивности, емкости и сопротивлении равна нулю для любого момента времени:

или, поскольку,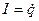

.

Введя обозначение

,

этому уравнению можно придать вид:

,

где .

Решение полученного уравнения имеет вид:

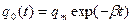где

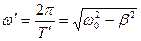Мы видим, что частота свободных затухающих колебаний ω^′ меньше собственной частоты ω₀. Подставив значения ω₀ и β, получим:

Амплитуда затухающих колебаний заряда конденсатора q₀(t) уменьшается со временем по экспоненциальному закону (рис.16.4). Коэффициент β называется коэффициентом затухания.

Рис.16.4. Изменение заряда конденсатора со временем в RLC-контуре.

Затухание колебаний принято характеризовать декрементом колебаний λ, определяемым как:

.

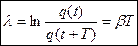Легко видеть, что декремент колебаний обратен по величине числу колебаний N_e, совершаемых за время, в течение которого амплитуда колебаний уменьшается в е раз: λ=1/N_e. Добротностью колебательного контура называется величина:

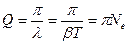
Из этой формулы видно, что добротность тем выше, чем меньше коэффициент затухания β. При малых затуханиях (λ<<1) можно приближенно считать, что

.

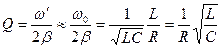Амплитуда тока в контуре, как и заряд на конденсаторе, убывает со временем по закону . Энергия W, запасенная в контуре, пропорциональна квадрату амплитуды тока (или квадрату напряжения на конденсаторе). Следовательно, W убывает со временем по закону e^-2βt. Относительное уменьшение энергии за период колебания Т (при малом затухании) есть:

.

Таким образом, потери энергии в колебательном контуре тем меньше, чем выше его добротность.

Дата добавления: 2014-01-07