Деревья

Теперь обратимся к изучению деревьев, наиболее важных нелинейных структур, встречающихся в вычислительных алгоритмах. Грубо говоря, структура дерева означает "разветвление", такое отношение между "узлами", как и в обычных деревьях.

Дерево - одна из самых распространенных структур, используемых для представления данных в ЭВМ. А вообще, дерево - конечное множество, состоящее из одного или более элементов, называемых узлами.

Между узлами существует отношение типа "исходный-порождённый". Корень - узел, не имеющий исходного (отца). Все узлы, кроме корня, имеют только один исходный (исх.отца). Есть деревья, состоящие из одного корня. Каждый узел может иметь несколько порождённых (сыновей). Отношение "исходный-порождённый" действует только так: не бывает отношения "порождённый-исходный", т.к потомок узла никогда не станет его предком.

Сетевые структуры широко применяются при организации банков данных, систем управления базами данных, в системах программного имитационного моделирования сложных комплексов и т.д. Особое значение сетевые структуры приобрели в системах искусственного интеллекта, в которых они адекватно отражают логику организации данных и сложные отношения, возникающие в таких системах между различными элементами данных. В этих системах сетевые структуры применяются для построения семантических сетей, фреймов и других логических конструкций, необходимых для представления знаний, образования понятий и осуществления логических выводов.

Сетевые структуры – весьма общий и гибкий класс связных списков. Рассмотрим частные случаи многосвязных списков – древовидные структуры, или просто деревья.

Различное представление деревьев показано на рис. 1.1.

А))

		В
	С

Корни у деревьев могут располагаться в разных местах. Могут вверх (рис.1.1,а), могут вниз (рис. 1.1,в), могут слева или справа (рис. 1.1,с).

Определим формально дерево как конечное множество Т, состоящее из одного или более узлов, таких, что

а) имеется один специально обозначенный узел, называемый корнем данного дерева,

б)остальные узлы (исключая корень) содержатся в m³0 попарно непересекающихся множествах Т₁, …, Т_m, каждое из которых в свою очередь является деревом. Деревья Т₁, …, Т_m называются поддеревьями данного корня.

Из определения следует, что каждый узел дерева является корнем некоторого поддерева, которое содержится в этом дереве. Число поддеревьев данного узла называется степенью этого узла. Узел с нулевой степенью называется концевым узлом; иногда его называют листом. Неконцевые узлы часто называют узлами разветвления. Уровень узла по отношению к дереву Т определяется следующим образом: говорят, что корень имеет уровень 1, а другие узлы имеют уровень на 1 выше их уровня относительно содержащего их поддерева Т_j этого корня.

Если в пункте б) определения имеет значение относительный порядок поддеревьев Т₁, …, Т_m, то говорят, что дерево является упорядоченным. Если два дерева, отличающиеся друг от друга только относительным порядком поддеревьев узлов, не считать различными, то в этом случае говорят, что дерево является ориентированным, поскольку здесь имеет значение только относительная ориентация узла, а не их порядок.

Лес – это множество (обычно упорядоченное), состоящее из некоторого (быть может равного нулю) числа непересекающихся деревьев. Пункт б) определения дерева можно сформулировать иначе, сказав, что узлы дерева, за исключением корня, образуют лес.

Деревья, как правило, дают хорошее представление о структуре отношения между элементами данных.

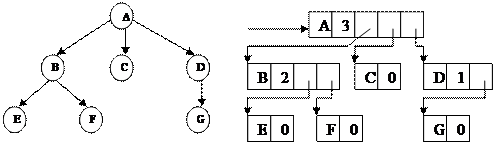Рис. 1.2. Представление графа в форме многосвязного списка

Обычно дерево представляется в машинной памяти в форме многосвязного списка, в котором каждый указатель соответствует дуге. Это представление называется естественным представлением дерева. Существуют несколько разновидностей такого представления. В одной из наиболее общих разновидностей каждому узлу дерева ставится в соответствие элемент многосвязного списка, причем в каждом элементе отводятся следующие поля: поле данных, поле степени исхода (т.е. числа сыновей) и поля указателей, число которых равно степени исхода. На рисунке дан пример дерева и представление этого дерева в виде многосвязного списка, начало которого, соответствующее корню дерева, адресуется указателем Р. Предполагается, что этот указатель входит в дескриптор, содержащий и другую общую информацию о списке (например, число элементов). Обозначения А, В, С, D, E, F, записанные в первом поле каждого элемента списка, представляют собой данные о соответствующих узлах дерева.

В некоторых случаях используется и последовательное представление деревьев в памяти. Такой способ может быть рекомендован, например, в случае постоянства или редкой изменчивости структуры дерева.

Дата добавления: 2014-01-07