
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Основные правила анализа алгоритмов
|
|
|
|
Основным критерием эффективности алгоритма является его временная сложность. При нахождении времени выполнения итеративных и рекурсивных алгоритмов используют различные методы и приемы, опирающиеся на некоторые базовые принципы.
Пусть  и
и  ‑ время выполнения двух фрагментов
‑ время выполнения двух фрагментов  и
и  ,
,  имеет степень роста
имеет степень роста , а
, а  ‑
‑  . Тогда
. Тогда  , т.е. время последовательного выполнения фрагментов
, т.е. время последовательного выполнения фрагментов  и
и , имеет степень роста
, имеет степень роста  .
.
Правило сумм, данное выше, используется для вычисления времени последовательного выполнения программных фрагментов с циклами и ветвлениями. Пусть есть три фрагмента с временами выполнения соответственно 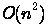 ,
,  и
и  (под обозначением
(под обозначением  мы будем понимать двоичный логарифм). Тогда время последовательного выполнения всех трех фрагментов имеет порядок
мы будем понимать двоичный логарифм). Тогда время последовательного выполнения всех трех фрагментов имеет порядок  , это то же самое, что
, это то же самое, что  . В общем случае время выполнения конечной последовательности фрагментов алгоритма, без учета констант, имеет порядок фрагмента с наибольшим временем выполнения. Иногда возможна ситуация, когда порядки роста времен нескольких фрагментов несоизмеримы (ни один из них не больше, чем другой, но они и не равны). Для примера рассмотрим два фрагмента с временем выполнения O(f(n)) и O(g(n)), где
. В общем случае время выполнения конечной последовательности фрагментов алгоритма, без учета констант, имеет порядок фрагмента с наибольшим временем выполнения. Иногда возможна ситуация, когда порядки роста времен нескольких фрагментов несоизмеримы (ни один из них не больше, чем другой, но они и не равны). Для примера рассмотрим два фрагмента с временем выполнения O(f(n)) и O(g(n)), где


В данном случае правило сумм можно применить непосредственно и получить время выполнения  , т.е. п 4 при п четном и п 3, если п нечетно. Из правила сумм также следует, что если
, т.е. п 4 при п четном и п 3, если п нечетно. Из правила сумм также следует, что если 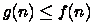 для всех п, превышающих п 0, то выражение
для всех п, превышающих п 0, то выражение  эквивалентно
эквивалентно  . Например,
. Например,  то же самое что
то же самое что 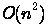 .
.
Правило произведений заключается в следующем. Если  и
и  имеют степени роста
имеют степени роста 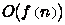 и
и  соответственно, то произведение
соответственно, то произведение 
 имеет степень роста
имеет степень роста  . Из правила произведений следует, что
. Из правила произведений следует, что 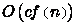 эквивалентно
эквивалентно 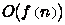 , если с — положительная константа. Например,
, если с — положительная константа. Например,  эквивалентно
эквивалентно 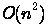 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 778; Нарушение авторских прав?; Мы поможем в написании вашей работы!