Некоторые задачи, где можно применить рекурсию

Задача 1. Вычисление факториала целого положительного числа n.

Для решения будем использовать равенства 0!=1, n!= n·(n-1)!

long Factorial(int n)

{

return n>1? n * Factorial(n-1) \ // if n > 1

: 1; // if n <= 1

}

Обратите внимание на некоторую двойственность использования имени factorial внутри описания функции: оно обозначает как переменную, так и вызываемую рекурсивно функцию. К счастью, в нашем случае они различаются по скобкам после имени, но если бы функция была без параметров, то дело было бы плохо. (Стандартная, но трудно находимая ошибка возникает, если автор полагает, что он использует значение переменной, а компилятор в этом месте видит рекурсивный вызов.)

Задача 2. Написать рекурсивную функцию вычисления xⁿ, где n 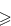0.

Для решения будем использовать равенства xⁿ = 1, при n = 0, и xⁿ =x·x^n-1, при n >0.

long Step(int x, int s)

{

return s>0? x * Step(x, s-1): 1;

}

Задача 3. Ханойские башни.
Когда-то в Ханое стоял храм и рядом с ним три башни (столба). На первую башню надеты 64 диска разного диаметра: самый большой - внизу, а самый маленький - вверху. Монахи этого храма должны были перенести все диски с первого столба на третий, соблюдая следующие правила:

1). можно перемещать только по одному диску;

2). больший диск нельзя класть на меньший;

3). снятый диск нельзя отложить, его необходимо сразу надеть на другой столб.

Предположим, с первого столба А надо перенести на третий С n дисков. Диски пронумерованы в порядке возрастания их диаметров. Предположим, что мы умеем переносить n -1 дисков. В этом случае n дисков перенесем посредством следующих шагов:

1) верхние n -1 дисков перенесем с первого на второй, пользуясь свободным третьим столбом;

2) последний диск наденем на третий столб;

3) n -1 дисков перенесем на третий, пользуясь свободным первым столбом.

Аналогичным образом можно перенести n -1, n -2 и т.д. дисков. Когда n =1, перенос осуществляется непосредственно с первого столба на третий.

void Move(int n, char a, char b, char c)

{

if(n > 0)

{

Move(n-1, a, c, b);

printf("%d -> %d ", a, c);

Move(n-1, b, a, c);

}

}

int main()

{ Move(3, 1, 2, 3);

return 0;

} Напишем рекурсивную процедуру перемещения i верхних колец с m -го стержня на n -й (предполагается, что остальные кольца больше по размеру и лежат на стержнях без движения).

void Move(int i, int m, int n)

{

if(i == 1) printf("Can move %d -> %d\n", m, n);

else

{

int s = 6 - m - n; // s - третий стержень: сумма номеров равна 6

Move(i-1, m,s);

printf("Can move %d -> %d\n", m, n);

Move(i-1, s, n);

}

} (Сначала переносится пирамидка из i -1 колец на третью палочку.После этого i -е кольцо освобождается, и его можно перенести куда следует. Остается положить на него пирамидку.)

Задача 4. Вывести все сочетания из n по k.

При вводе задается набор символов в виде строки. Длина строки len = n. Затем вводится число k.

#include <iostream>

typedef unsigned char byte;

std::string s, ss;

byte k, n, ii;

int num, count;

void Cmn(std::string q, byte i, byte j)

{

int len;

char ch;

while(count <= n)

{

q.assign((char*)&s[j], 1); // в стек заносятся элементы по одному

count++;

Cmn(q, 0, j+1);

}

Label:

len = q.size();

if(len < k)

if(j+i <= n) Cmn(q, i+1, j);

if(len < k && j+i <= n)

if(q[len]!= s[j+i])

{

q.insert(q.size(), (char*)&s[j+i], 1);

goto Label;

}

if(q.size() == k)

{

printf("%s: %d ", q.c_str(), num);

num++;

}

}

int main()

{

num = 1;

char chh[] = "12345"; // эдементы

k = n = strlen(chh); // количество элементов

s.assign(chh, n);

count = 1;

Cmn(std::string(), 0, 0); return 0;}

Задача 5. Перечислить все способы расстановки n ферзей на шахматной доске n×n, при которых они не бьют друг друга.

const int N = 8;

int x[N+1]; // индекс - номер ферзя, то есть номер вертикали bool a[N+1]; // занятость горизонтали, где индекс массива номер горизонталиbool b[ (N-1)*2 + 1 ]; /* номер диагонали определяется разностью индексов квадратной матрицы i-j, а диагонали параллельны главной диагонали матрицы */ bool c[ N*2+1 ]; /* номер диагонали определяется суммой

индексов i+j, а диагонали параллельны вспомогательной */

int Count; // номер варианта расстановки ферзей

void Print()

{

Count++;

for(int k = 0; k<N; k++) printf("%d..",x[k]);

printf("%d\n", Count);

char ch;

if(Count % 24 == 0) { printf(" Press Enter...");gets(&ch); }

}

void Try(int i)

{

for(int j=1; j<=N; j++)

if(a[j] && b[ i-j + (N-1) ] && c[i+j]) // если клетка не бьется, то

{

x[i] = j; // то ферзю i устанавливается номер горизонтали j

// соответствующие горизонтали и две вертикали становятся занятыми

a[j] = false;

b[ i-j + (N-1) ] = false;

c[i+j] = false;

/* если это не последний ферзь, то пытаемся поставить следующий ферзь, иначе распечатка варианта*/

if(i<n) Try(i+1);

else Print();

/* если нет небитого поля для данного ферзя, то предыдущая занятая позиция освобождается (отход назад) и все повторяется */

a[j] = true;

b[ i-j + (N-1) ] = true;

c[i+j] = true;

}

}

void Init()

{

Count = 0;

/* Все элементы логических массивов a,b,c становятся TRUE (1), то есть клетки доски не находятся под боем */

for(int i=0; i< N+1; i++) a[i] = true;

for(int i=0; i< (N-1)*2 + 1; i++) b[i] = true;

for(int i=0; i< N*2+1; i++) c[i] = true;

// все ферзи вне доски, то есть все x[i]=0

for(int i=0; i< N+1; i++) x[i] = 0;

}

int main()

{

Init();

Try(1);

return 0;

}

При анализе рекурсивной программы возникает, как обычно, двавопроса: (а) почему программа заканчивает работу? (б) почему она работает правильно, если заканчивает работу? Для (б) достаточно проверить, что (содержащая рекурсивный вызов) программа работает правильно, предположив, что вызываемая ею одноименная программа работает правильно. В самом деле, в этом случае в цепочке рекурсивно вызываемых программ все программы работают правильно (убеждаемся в этом, идя от конца цепочки к началу). Чтобы доказать (а), обычно проверяют, что с каждым рекурсивным вызовом значение какого-то параметра уменьшается, и это не может продолжаться бесконечно.

Дата добавления: 2014-01-07