Операции. Физическая структура

Физическая структура

Логическая структура

Массивы

Массив - такая структура данных, которая характеризуется:

- фиксированным набором элементов одного и того же типа;

- каждый элемент имеет уникальный набор значений индексов;

- количество индексов определяет мерность массива, например, два индекса - двумерный массив, три индекса - трехмерный массив, один индекс - одномерный массив или вектор;

- обращение к элементу массива выполняется по имени массива и значениям индексов для данного элемента.

Другое определение: массив - это вектор, каждый элемент которого - вектор.

Синтаксис описания массива представляется в виде:

<Тип> <Имя>[n1] [n2].. [nn];

Для случая двумерного массива:

<Тип> <Имя>[n1] [n2]

Наглядно двумерный массив можно представить в виде таблицы из n1 строк и n2 столбцов.

Физическая структура - это размещение элементов массива в памяти ЭВМ. Для случая двумерного массива, состоящего из (n) строк и (k) столбцов, физическая структура представлена на рис. 3.3.

@Mas	+0 ┌──┴──┐	+Sizeof(тип) ┌──┴──┐		+(k-1)* Sizeof(тип) ┌──┴──┐
	Mas[0][0]	Mas[0][1]	…	Mas[0][k-1]
	…	…		…
	Mas[n-1][0]	Mas[n-1][1]	…	Mas[n-1][k-1]
	+k*(n-1)* Sizeof(тип) или *(Mas+n-1)	+(k*(n-1)+1)* Sizeof(тип) или *(*(Mas+n-1)+1)		+(k*(n-1)+(k-1))* Sizeof(тип) или *(*(Mas+n-1)+k-1)

Рис. 3.1. Физическая структура двумерного массива из

(n) строк и (k) столбцов

Многомерные массивы хранятся в непрерывной области памяти. Размер слота определяется базовым типом элемента массива. Количество элементов массива и размер слота определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так, в FORTRAN элементы распределяются по столбцам - так, что быстрее меняются левые индексы, в PASCAL - по строкам - изменение индексов выполняется в направлении справа налево.

Количество байтов памяти, занятых двумерным массивом, определяется по формуле:

ByteSize = (n)*(k)*SizeOf(Тип) (3.1)

Адресом массива является адрес первого байта начального компонента массива. Смещение к элементу массива Mas[i1][i2] определяется по формуле:

ByteNumber = [ i1* k + i2 ]*SizeOf(Тип) (3.2)

его адрес: @ByteNumber = @mas + ByteNumber = *(*(Mas + i1) + i2)

Например:

short Mas[3][2];

Базовый тип элемента short требует два байта памяти, тогда табл. 3.1 смещений элементов массива относительно @Mas будет выглядеть так:

Таблица 3.1

Смещение, байт	Элемент массива	Смещениие, байт	Элемент массива
+0	Mas[0,0]	+2	Mas[0,1]
+4	Mas[1,0]	+6	Mas[1,1]
+8	Mas[2,0]	+10	Mas[2,1]

Этот массив будет занимать в памяти: 3*2*2=12 байт; а адрес элемента Mas[2,1]: @Mas+(1*2+1)*2 = @Mas+6 = *(*(Mas +2) +1)

Важнейшая операция физического уровня над массивом - доступ к заданному элементу. Как только реализован доступ к элементу, над ним может быть выполнена любая операция, имеющая смысл для того типа данных, которому соответствует элемент. Преобразование логической структуры в физическую, в ходе которого многомерная логическая структура массива преобразуется в одномерную физическую структуру, называется процессом линеаризации.

В соответствии с формулами (3.1), (3.2) и по аналогии с вектором (2.1), (2.2) для двумерного массива с границами изменения индексов:

[ B(1) ][ B(2) ], размещенного в памяти по строкам, адрес элемента с индексами [I(1),I(2)] может быть вычислен как:

Addr[I(1),I(2)] = *(*(Addr+I(1)) + I(2)) (3.3)

Обобщая (3.3) для массива произвольной размерности:

Mas[B(1)][B(2)]...[B(n)], получим

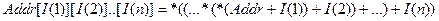, (3.4)

Одно из определений массива гласит, что это вектор, каждый элемент которого - вектор. Некоторые языки программирования позволяют выделить из многомерного массива одно или несколько измерений и рассматривать их как массив меньшей мерности.

Например: если в PL/1 - программе объявлен двумерный массив:

DECLARE A(10,10) BINARY FIXED;

то выражение A[*,I] - будет обращаться к одномерному массиву, состоящему из элементов: A(1,I), A(2,I),...,A(10,I).

Символ-джокер "*" означает, что выбираются все элементы массива по тому измерению, которому соответствует заданный джокером индекс. Использование джокера позволяет также задавать групповые операции над всеми элементами массива или над выбранным его измерением, например: A(*,I) = A(*,I) + 1.

К операциям логического уровня над массивами необходимо отнести такие, как сортировка массива, поиск элемента по ключу. Наиболее распространенные алгоритмы поиска и сортировок будут рассмотрены в данной главе ниже.

Дата добавления: 2014-01-07