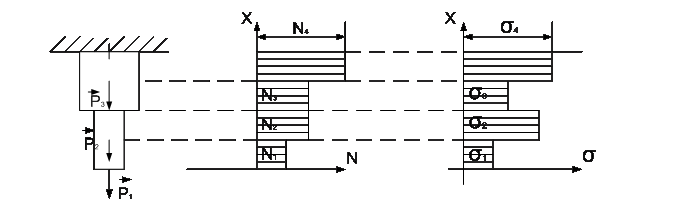
Растяжение и сжатие

Во многих случаях собственный вес частей машин и сооружений весьма мал по сравнению с приложенными нагрузками. Поэтому в этих задачах не учитывают действие собственного веса, что упрощает расчет и дает очень малую ошибку в результаты.

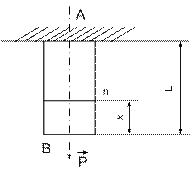
Рассмотрим призматический стержень (т.е. прямой стержень постоянного сечения F), закрепленный верхним концом в сечении А и нагруженный осевой силой на нижнем конце. Проведем произвольное сечение n, перпендикулярное к оси стержня и расположенное на расстоянии х от нижнего конца. Отбросим верхнюю часть стержня и рассмотрим равновесие оставшейся нижней части. По сечению будут действовать напряжения, заменяющие действие отброшенной верхней части на нижнюю. Возникает вопрос о том, по какому закону эти напряжения распределены по данному сечению. Произведя растяжение стержней с различной формой поперечного сечения, сплошных и трубчатых, и измеряя деформацию в различных точках разных поперечных сечений, можно практически убедиться в том, что в данном случае все элементы стержня деформируются одинаково. Поэтому можно сделать вывод, что напряжения по сечению распределены равномерно и что эти напряжения параллельны действующему усилию. Из уравнения равновесия для отсеченной части стержня находим продольную силу в сечении , т.е. продольная сила во всех сечениях данного стержня имеет постоянную величину. В силу гипотезы о равномерном распределении напряжений по сечению стержня можно написать

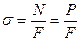или (1)

Формула (1) применяется в теории растяжения или сжатия призматических стержней без учета собственного веса. Вычислив по этой формуле напряжения в поперечном сечении стержня, нужно оценить данное напряженное состояние с точки зрения его опасности или безопасности для нормальной эксплуатации машины или сооружения. Допустим что мы имеем возможность неограниченно увеличивать силу . В таком случае после достижения максимального значения Р_мах произойдет разрушение стержня. Отнеся силу Р_мах к начальной площади поперечного сечения стержня, получим так называемый предел прочности материала, или временное сопротивление разрыву

(2)

Пределом прочности материала или его временным сопротивлением разрыву называется условное напряжение, вычисляемое делением максимального растягивающего усилия на первоначальную площадь поперечного стержня при его разрыве.

Эта характеристика – одна из важнейших при оценке инженерных качеств того или иного материала. Ясно, что в нормально работающей длительное время детали, которая не должна ни разрушаться, ни сильно деформироваться под действием рабочих усилий, действующее напряжение должно быть меньше предела прочности материала. Длительный опыт эксплуатации различных машин и некоторые теоретические соображения показывают, что для нормальной работы детали действующее в ней напряжение не должно превышать части от предела прочности. Эта часть предела прочности получила название допускаемого напряжения и условно обозначается []: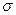

; к >1 (3

Правильный выбор величины к, которая в свою очередь получила название общего запаса прочности или общего коэффициента безопасности, представляет весьма ответственную и трудную задачу. Чтобы облегчить работу конструктора или эксплуатационника при изготовлении или эксплуатации многих машин, в специальных технических нормах установлены допускаемые напряжения. Тем самым ответственность за правильный выбор этой величины возлагается на ту научно-техническую организацию, которая утвердила указанные выше нормы.

Расчеты на прочность и жесткость

1. Если известно допускаемое напряжение , то можно оценить напряженное состояние рассчитываемой детали по формуле

(4)

Эта формула называется формулой проверки прочности.

2. Если ее решить относительно действующей силы , то получится второй вид этого уравнения, которое называется формулой проверки предельной (допускаемой) нагрузки

(5)

3. Наконец, если решить уравнение (4) относительно площади поперечного сечения F, то получится третий его вид, который может быть назван формулой определения необходимых размеров по условию прочности.

(6)

В сопротивлении материалов весьма распространен метод графической иллюстрации полученных решений. Так, например, для рассматриваемой задачи можно построить эпюры продольных сил и напряжений вдоль стержня. Эпюра продольных сил – это график, выявляющий зависимость действующей в поперечном сечении стержня продольной силы от положения сечения. Для данной задачи продольная сила определяется уравнением 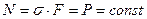. В данной задаче и продольная сила и напряжение в поперечном сечении 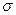не зависят от координаты х. В других задачах этого может не быть Сечение с наибольшим напряжением называется опасным.

Если сечение стержня переменно или продольная сила в различных сечениях стержня имеет разные значения, то вместо формулы (1) надо написать

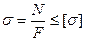
Это выражение применяется для расчета опасного сечения, т.е. сечения в котором напряжение получается наибольшим.

Опасное сечение определяется конкретными числовыми данными и может оказаться в изображенном на рисунке примере на втором или четвертом участке.

Рассмотрев вопрос о напряжениях, обратимся к изучению деформации при растяжении-сжатии. Если расчет по напряжениям называется расчетом на прочность, то расчет по деформациям – расчетом на жесткость. В основе этого изучения лежит установленный опытным путем закон Гука. В общем виде этот закон гласит: в определенных пределах деформации пропорциональны действующим усилиям. Применительно к случаю растяжения призматического стержня без учета собственного веса закон Гука выражается формулой:

(6)

т.е. абсолютное удлинение стержня прямо пропорционально действующей силе и длине стержня и обратно пропорционально площади поперечного сечения и коэффициенту Е, называемому модулем упругости первого рода, или модулем Юнга (модулем продольной упругости). Формулу (6) можно назвать формулой закона Гука в абсолютных единицах. Если использовать понятие относительного удлинения , то формулу (6) с учетом формулы (1) можно записать в виде

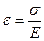(7)

Относительное удлинение есть величина безразмерная. Поэтому модуль продольной упругости Е имеет размерность напряжения. Если решить формулу (7) относительно Е, то получим Отсюда вытекает одно из возможных определений модуля продольной упругости: модулем продольной упругости для данного материала называется отношение нормального напряжения к вызванному им относительному удлинению в пределах справедливости закона Гука. Этот коэффициент является весьма важной физической константой материала и для всех основных материалов дается в справочной литературе. Для большинства механических расчетов модуль продольной упругости: для стали Е=2*10⁵ н/мм²; для меди Е=1*10⁵н/мм²; для чугуна Е=1,3*10⁵н/мм²; для алюминия Е=0,7*10⁵н/мм²; для ковкого чугуна Е=1,55*10⁵н/мм²; для латуни Е=1*10⁵н/мм².

Механические свойства материалов

Для расчета стержня на прочность и на жесткость надо знать некоторые свойства данного материала. Все физические характеристики, имеющие отношение к данному вопросу, называются механическими характеристиками материала. Основные – предельные напряжения, твердость, ударная вязкость. Механические характеристики материалов определяются с помощью их испытания. Рассмотрим испытания на разрыв стали. Для испытания необходимо иметь машину, в которой можно закрепить образец определенной формы и непрерывным и плавным повышением приложенной к нему нагрузки довести до разрушения. Под действием постепенно возрастающей нагрузки длина образца также непрерывно увеличивается. Современные испытательные машины автоматически записывают диаграмму зависимости абсолютного удлинения от растягивающей силы .

Недостатком этой диаграммы является ее очевидная зависимость не только от свойств материала, но и от размеров испытываемого образца. Поэтому диаграмму растяжения перестраивают в осях , где 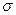- условное напряжение 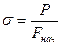, а - относительное удлинение . Новая диаграмма называется диаграммой условных напряжений при растяжении. Напряжения являются условными, так как сила делится на начальную площадь поперечного сечения, а не на действительную.

Изучение диаграммы условных напряжений дает много сведений о свойствах материала. В точке А напряжение носит название предела пропорциональности и обозначается

Пределом пропорциональности называется напряжение, при котором замечается отклонение от законов Гука.

В точке С проявляется новое свойство мягкой стали: замечается рост деформации при постоянной нагрузке, что приводит к образованию на диаграмме после точки С горизонтальной площадки.

Напряжение, при котором наблюдается внезапное увеличение деформации при постоянной нагрузке, называется физическим пределом текучести материала и обозначается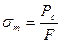

Рост деформации при постоянной нагрузке по достижению некоторой величины прекращается, и для дальнейшего увеличения деформации необходимо снова повысить нагрузку. Это явление получило название упрочнения. Точке D диаграммы соответствует наибольшей достигнутой за время испытания нагрузке.

В этот момент на образце начинает образовываться местное уточнение, называемое шейкой. Вся дальнейшая деформация происходит только в области шейки, площадь поперечного сечения быстро уменьшается, в связи с чем рост деформации происходит при уменьшающейся нагрузке. Условное напряжение, получаемое делением наибольшей достигнутой за время испытания силы на первоначальную площадь поперечного сечения, называется пределом прочности материала, или временным сопротивлением разрыву и обозначается или 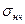. В точке R происходит разрыв образца.

При нагрузке постепенно увеличивающимися ступенями с обязательной разгрузкой в конце каждой ступени при некотором напряжении, соответствующем точке В диаграммы будет замечено появление остаточных деформаций. Напряжение, при котором появляются остаточные деформации, называется пределом упругости и обозначается

Если в процессе нагружения образца было достигнуто напряжение, соответствующее точке К, а затем была произведена разгрузка, то в процессе разгрузки деформация изменяется по прямой КN. Следовательно, общая достигнутая к моменту начала разгрузки деформация , распадается на две: упругую, или исчезающую и пластическую, или остаточную : =+

Прямая KN показывает, что упругая часть общей деформации и за пределами упругости продолжает следовать закону Гука и может быть вычислена по формуле

Это явление носит название закона разгрузки или закона Герстнера. Если получивший пластическую деформацию разгруженный до нуля образец будет вновь нагружен, то линия повторного напряжения будет изображаться сначала прямой NK, а затем после точки К деформация снова будет следовать зависимости, изображенной кривой KDE. Если свойства материала оцениваются по данным повторного нагружения, то пределы пропорциональности упругости и условный предел текучести повышаются, пластичные свойства материала уменьшаются, твердость и хрупкость возрастают. Явление изменения механических свойств материала, вызванного остаточной деформацией его при обычной (комнатной) температуре, получило название наклепа или нагартовки. Наклеп может быть и полезным и вредным явлением в зависимости от условий работы детали.

Твердость материалов

Испытание образцов на растяжение и сжатие дает объективную оценку свойств материала. В производстве, однако, для оперативного контроля за качеством изготовляемых деталей этот метод испытания представляет в ряде случаев значительные неудобства. На практике прибегают к сравнительной оценке свойств материала при помощи пробы на твердость. Под твердостью понимается способность материала противодействовать механическому проникновению в него посторонних тел. Такое определение твердости, по существу повторяет определение свойства прочности. В материале при вдавливании в него острого предмета возникают местные пластические деформации, сопровождающиеся при дальнейшем увеличении сил местным разрушением. Поэтому показатель твердости связан с показателем прочности и пластичности и зависит от конкретных условий ведения испытания.

Наиболее широкое распространение получили пробы по Бринеллю и по Роквеллу. В первом случае в поверхность исследуемой детали вдавливается стальной шарик, во втором – алмазный наконечник. По обмеру полученного отпечатка судят о твердости материала. При помощи переводных таблиц приближенно по показателю твердости определяют предел прочности материала. Таким образом, в результате пробы на твердость удается определить прочностные показатели материала, не разрушая детали.

Одной из основных технологических операций позволяющих измерить в нужном направлении свойства материала, является термообработка. Например, закалка резко повышает прочностные характеристики стали и одновременно снижает ее пластические свойства. Для большинства широко применяемых в машиностроении материалов хорошо известны те режимы термообработки, которые обеспечивают получение необходимых механических характеристик материала.

Кручение

Непосредственный эксперимент, проводимый в пределах пропорциональности, показывает следующее:

1. Длина стержня, а также расстояние между любыми двумя соседними поперечными окружностями, нанесенными на стержне, остаются без изменения;

2. Диаметр стержня также не изменяется и, следовательно, не изменяется объем стержня;

3. Правое концевое сечение поворачивается относительно левого на некоторый угол φ, называемый углом закручивания; два смежных сечения расположенных на расстоянии dx друг от друга, поворачиваются взаимно на угол dφ; величина 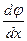, являющаяся относительным углом закручивания, оказывается постоянной, т.е. деформация кручения равномерно распределяется по длине стержня;

4.Производя испытания на скручивание цилиндрических образцов различных образцов различных размеров, изготовленных из одного и того же материала, можно на основании найденных при испытании данных получить формулу:

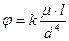(1)

эта формула – закон Гука при кручении. Входящий в формулу коэффициент к зависит от материала стержня.

При кручении действуют только касательные напряжения, поэтому проверка прочности проводится по формуле:

(2)

где М – крутящий момент, r – радиус стержня, а I_p – полярный момент инерции сечения, вычисляемый по формуле (ρ – радиус, определяющий расстояние от полюса О до элементарной площади dF). Для круглого сечения

Обычно выражение I_p/r обозначают одним символом W_p и называют эту характеристику поперечного сечения (имеющую размерность длины в кубе) полярным моментом сопротивления сечения. Для круглого сечения

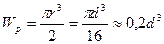
Уравнение (2) можно переписать в более простом виде:

(3)

Решая выражение (3) относительно μ, получим формулу проверки грузоподъемности стержня по условию прочности:

Наконец, подставляя вместо W_p его значение и решая относительно d, получим формулу определения необходимых размеров по условию прочности:

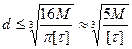
Построение эпюр крутящих моментов

Детали (валы) машин и механизмов подвергаются действию многочисленных факторов, приложенных в различных местах по длине стержня. При построении эпюры крутящих моментов обычно отвлекаются от действия изгибающих силовых факторов и рассматривают действия только крутящих моментов.

В состоянии установившего движения μ₀= μ₁+ μ₂+ μ₃; где μ₀ – момент ведущего шкива, μ₁, μ₂, μ₃ – моменты ведомых шкивов. При построении эпюр крутящих моментов какое-то направление приложенных к шкивам моментов принимают за положительное, а противоположное за отрицательное. Знак момента на имеет никакого значения для расчета на прочность.

Кручение некруглых стержней

Оказывается, что при кручении некруглых стержней формулы расчета на прочность и на жесткость имеют вид:

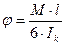
В этих формулах W_k – момент сопротивления сечения при кручении I_k – момент жесткости сечения при кручении. Обе величины берутся из справочной литературы. Например, для сечения в форме узкого прямоугольника при отношении сторон h/b>10 можно принять

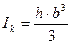
Изгиб

Как было указано ранее, изгиб стержня вызывается силами, действующими перпендикулярно к оси стержня и удаленными достаточно далеко друг от друга. Подвергающаяся действию внешних сил (нагрузок) балка должна быть в пространстве геометрически неизменяема (если не учитывать ее деформации). Для этого она должна быть каким-то образом закреплена. Устройства, с помощью которых балка прикрепляется к другим телам, принимаемым за неподвижные, называются опорными устройствами, или кратко – опорами.

Имеются три наиболее распространенных типа опор:

- шарнирно-подвижная опора;

- шарнирно-неподвижная опора;

- жесткая заделка.

Шарнирно-подвижная опора отнимает у балки одну степень свободы, а возникающая в ней реакция имеет одну неизвестную – величину реактивной силы, которая перпендикулярна к поверхности катания (скольжения).

Шарнирно-неподвижная опора уничтожает две степени свободы у балки и имеет две неизвестные реактивные силы – перпендикулярную и параллельную оси балки.

Жесткая заделка отнимает три степени свободы у балки. И имеет три неизвестных силовых фактора: две силы перпендикулярные и параллельные оси балки и пара сил с моментом М_p.

Изгибающий момент и поперечная сила

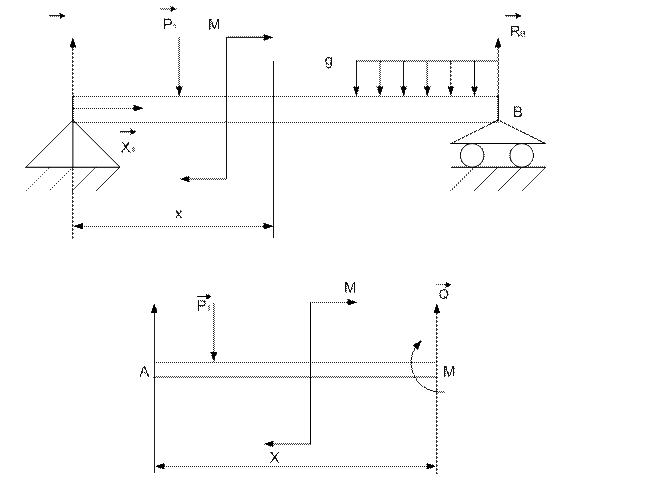
Для расчета на прочность при изгибе необходимо научиться определять действующие в любом сечении балки силовые факторы. Рассмотрим балку АВ:

Проведя произвольное сечение на расстоянии х от левого конца балки, изображаем отсеченную левую часть балки отдельно, показывая все приложенные к ней нагрузки и реактивные силы, т.е. все внешние силовые факторы, действующие слева от сечения. Из условий равновесия левой части получим:

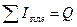
(1)

где Q – поперечная сила в данном сечении балки, равная сумме проекций всех сил, расположенных по одну сторону от сечения, перпендикулярного к оси балки прямую, лежащую в силовой плоскости.

М – изгибающий момент в данном сечении балки, равен сумме моментов всех сил, расположенных по одну сторону от сечения, относительно центра тяжести сечения.

При установлении соотношений (1) была рассмотрена левая отсеченная часть балки. Однако такой же результат легко можно получить, рассматривая правую часть балки, так как вся балка находится в равновесии, т.е. поперечная сила и изгибающий момент в данном сечении балки не зависят от того, какую часть балки рассматривают – левую или правую. В отношении знака, приписываемого этим силовым фактором надо сделать следующее значение. Знак должен указывать на характер деформации, вызываемой данным силовым фактором. Одинаковому характеру деформации должен соответствовать одинаковый знак силового фактора. Изгибающему моменту, вызывающему искривление балки выпуклостью вниз условились приписывать знак +. Отсюда вытекает правило знаков для изгибающего момента, которое может быть сформулировано в двух вариантах:

1. Изгибающий момент считается положительным, если он стремится вращать левую часть балки по часовой или правую против;

2. Изгибающий момент положителен, если он гнет балку выпуклостью вниз.

Аналогично установлено и правило знаков для поперечной силы: поперечная сила считается положительной, если она стремится сдвинуть левую часть балки вверх, а правую вниз.

В общем случае величины и знаки изгибающего момента и поперечной силы в различных сечениях балки различны, т.е. они являются функциями координаты х: М=М(х); Q=Q(x).

Как и в других случаях, в целях наглядности принято строить эпюры изгибающего момента и поперечной силы. Эпюры не только наглядно показывают, как изменится та или иная величина вдоль по балке, но и сразу позволяют установить те сечения балки, где эти величины достигают своего наибольшего значения, а именно эти сечения могут быть наиболее опасными с точки зрения прочности, и потому их нахождение является весьма важной задачей.

Рассмотрим несколько примеров построения эпюр изгибающих моментов и поперечных сил.

Консоль АВ заделана в сечение В, а на конце А приложена сила . Проводим сечение на расстоянии х от левого конца балки и по данному определению составляем уравнение изгибающего момента и поперечной силы в сечении μ= -Рх Q= -P (2)

Начертив координатные оси μ-х и Q-x в соответствующем масштабе изображаем уравнение (2) графически. По эпюрам видно, что наибольший по абсолютной величине изгибающий момент имеет место в защемлении . Поперечная сила везде постоянна и равна по величине . Следовательно, опасным сечением балки является сечение в заделке.

Консоль АВ нагружена равномерно распределенной нагрузкой с интенсивностью g. В данном случае удобнее рассматривать правую часть балки а не левую. По определению получаем:

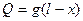
(3)

Из формулы (3) видно, что поперечная сила изображается наклонной прямой (т.к. х входит в первой степени), а изгибающий момент – параболой. Давая х значения О и l находим: 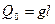,, , . Заметим, что знак d²M/dx², будет отрицательным при любом значении х, вогнутость кривой обращена вниз, а первая обращается в нуль при х=l, то есть в этом месте касательная к эпюре изгибающего момента горизонтальна. Опять видно, что опасное сечение балки оказалось в заделке.

Следует обратить внимание, что в обоих случаях рассматривалась та часть балки, на которой не было заделки. Поэтому предварительно можно было не находить опорных реакций. Они получились в данном случае автоматически по эпюрам μ и Q как соответствующие краевые значения этих функций.

Для этой балки избежать определения опорных реакций нельзя. Поэтому сначала необходимо их найти. . Определение μ и Q приходится в данном случае вести отдельно на каждом участке балке, т.к. с переходом на другой участок меняется число участвующих в деформации силовых факторов. Граница участка всегда создается появлением какого-либо нового силового фактора или исчезновением старого. Проводим сечение на первом участке и, рассматривая левую часть балки, получаем:

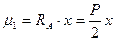
Вычисляем значения μ₁ в начале и в конце участка:

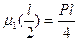
и строим по этим данном масштабе эпюры на участке 1.

Для участка 2, рассматривая правую часть балки, получаем, получаем:

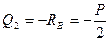
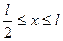
Аналогично предыдущему вычисляем:

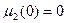
В разобранном примере абсцисса х отсчитывается от одного и того же начала координат, но это не обязательно – можно на каждом участке балке выбирать новую координатную систему.

Дифференциальные зависимости между силовыми факторами при изгибе. Опасные сечения

Между силовыми факторами, действующими в данном сечении балки, существуют определенные зависимости, которые могут быть сформулированы следующим образом:

1. Производная от изгибающего момента по х равна поперечной силе (теорема Журавского).

2. Производная от поперечной силы по х равна интенсивности сплошной (распределенной) нагрузки.

С учетом этого можно перечислить следующие признаки тех сечений, в которых изгибающий момент принимает наибольшее по абсолютной величине значение:

1) сечение, в котором поперечная сила равна нулю;

2) сечение, в котором поперечная сила скачком меняет свой знак на обратный;

3) сечение на одном из концов балки;

4) сечение, в котором приложена сосредоточенная пара сил.

На практике эпюры М и Q часто строятся без составления соответствующих уравнений для каждого участка балки, а лишь на основании общих соображений о форме линий, изображающих силовые факторы в сечении, и их ординатах в характерных точках (сечениях). К основным правилам при подобном построении и контроле правильности эпюр М и Q относятся следующие.

1. На участках балки, свободных от сплошной (распределенной) нагрузки, эпюра поперечных сил должна изображаться горизонтальными прямыми, а эпюра М – наклонными прямыми.

2. Там, где приложены сосредоточенные силы, эпюра Q имеет разрыв непрерывности на величину силы, а эпюра М – излом.

3. Там где приложена пара сил, эпюра Q сохраняет плавность и непрерывность, а эпюра μ имеет разрыв непрерывности на величину пары М, сохраняя постоянное направление касательной.

4. Начальные и конечные значения на эпюрах Q и М должны совпадать со значением сосредоточенных сил и пар, приложенных к концам балки (в частности, опорных реактивных силовых факторов) с учетом правила знаков.

5. На участках балки, несущих равномерно распределенную нагрузку эпюра Q изображается наклонной прямой, а эпюра М – квадратной параболой.

6. Там, где Q>0, изгибающий момент возрастает (по алгебраической величине), а там, где Q<0 – убывает.

Умение правильно строить эпюры М и Q имеет очень большое значение, так как на их основе выбирается опасное сечение балки и устанавливаются расчетные изгибающий момент и поперечная сила. Обычно опасным с точки зрения прочности балки оказывается сечение с наибольшим изгибающим моментом. Но иногда таким может оказаться сечение с наибольшей поперечной силой, а еще реже – какое-то промежуточное сечение между двумя указанными выше.

Напряжение при чистом изгибе

Чтобы упростить решение задачи начнем с такого случая изгиба, когда в поперечном сечении балки действует только один силовой фактор, а именно – изгибающий момент μ, а поперечная сила Q=0. Так как 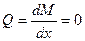, то в этом случае μ=const. Такой случай изгиба носит название чистого изгиба. При чистом изгибе характер деформации позволяет отметить следующие основные ее особенности.

1. Продольные прямые по боковой поверхности искривляются, обращаясь в дуги окружностей.

2. Поперечные прямые остаются прямыми, но взаимно наклоняются, принимая радиальное направление.

3. Поперечное сечение деформируется, причем непосредственное измерение продольной и поперечной деформации для одного и того же слоя волокон дает следующий результат:

4. На вогнутой стороне стержня продольные волокна укоротились, а на выпуклой стороне удлинились, следовательно, где-то между ними находится такой слой волокон, длина которых окажется без изменений. Этот слой называется нейтральным.

Выделим из балки после ее деформации двумя сечениями, перпендикулярным к оси балки, элемент, длина которого до деформации была равна dx. После деформации его боковые грани остались плоскими но повернутыми относительно друг друга на угол dφ радиус кривизны нейтрального слоя ef обозначим ρ. Рассмотрим деформацию произвольного волокна mn, положение которого внутри элемента определяется расстоянием у от нейтрального слоя. Это расстояние будем считать положительным в сторону выпуклости балки. В таком случае относительное удлинение произвольного волокна

Учитывая линейность напряженного состояния волокон балки, получаем по закону Гука (1)

Формула (1) устанавливает закон распределения нормальных напряжений по поперечному сечению балки. Этот закон оказывается линейным, то есть напряжения в сечении прямо пропорциональны расстоянию волокон от нейтрального слоя. Оказывается, что положение нейтрального слоя определяется осями YOZ, проходящими через центр тяжести поперечного сечения.

Для определения радиуса кривизны нейтрального слоя составим уравнение равновесия относительно оси OZ: или ;

Обозначив величину 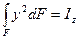, где I_z – осевой момент инерции сечения относительно оси OZ получим 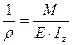(2) Подставив в формулу (1) выражение (2) получаем 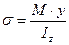(3).

Для крайних точек контура поперечного сечения А и В найдем:

;

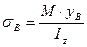
Как видно из эпюры напряжений в поперечном сечении, прочность балки при чистом изгибе должна проверятся в крайних точках сечения и в общем случае, если материал балки неодинаково работает на растяжение и сжатие, следует записать две формулы проверки прочности: на растяжение 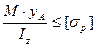; на сжатие: .

В тех случаях, когда у_A=|y_B|=y_макс, удобно ввести новую геометрическую характеристику сечения – момент сопротивления сечения при изгибе, равный отношению осевого момента инерции сечения относительно нейтральной оси к расстоянию до крайнего волокна.

Для круглого стержня

Для часто применяемых в практике профилей балок эта характеристика включена в таблицы стандартов. С помощью этого понятия уравнение проверки прочности при чистом изгибе может быть записано так

(4)

Приведенные формулы получены для случая чистого изгиба. Однако на практике чистый изгиб встречается относительно редко. Гораздо чаще встречается так называемый поперечный изгиб, при котором в каждом поперечном сечении балки, помимо изгибающего момента, есть еще и поперечная сила. Изгибающий момент в этом случае не остается постоянным в различных сечениях, а изменяется в соответствии с эпюрой изгибающего момента. Практика показывает, что в большинстве случаев бывает достаточно проверить прочность балки, подвергающейся поперечному изгибу, по нормальным напряжениям, которые при поперечном изгибе вычисляются по тем же формулам, что и при чистом изгибе. В этом случае проверку прочности надо делать по опасному сечению, то есть по тому сечению, в котором действует наибольший по абсолютной величине изгибающий момент (при постоянном сечении балки).

При подборе сечения балки с помощью уравнения (4) надо иметь в виду следующее. Вычислив необходимый момент сопротивления сечения и обратившись к сортаментной таблице указанного в условии профиля, мы как правило, не найдем там точно такого же значения W. Поэтому приходится брать либо ближайшее меньшее, либо ближайшее большее значение. Ближайшее меньшее значение можно брать лишь при условии, что оно отличается от необходимого не более чем на 5%. В противном случае надо выбирать ближайший больший номер профиля, независимо от отклонения табличного значения W от необходимого. Балка будет иметь в этом случае некоторый избыточный запас прочности.

Одновременное действие изгиба и кручения

Одновременное действие изгиба и кручения особенно часто подвергаются детали машин, передающие вращательное движение и называемое валами. В общем случае нагружения вала в отдельных сечениях вала будут существовать шесть силовых факторов: продольная сила N, две поперечные силы Q_y и Q_z, два изгибающих момента М_y и М_z и крутящий момент M_x. Для наглядности принято строить эпюры этих силовых факторов. Общая последовательность операций при построении эпюр такова. Сначала необходимо все внешние силы, приложенные к валу, привести к центрам тяжести соответствующих сечений. При этом поперечные силы разлагаются по направлениям осей YZ. Затем находятся опорные реакции отдельно для сил, лежащих в плоскости YOX () и для сил, лежащих в плоскости ZOX(). Далее, для сил, лежащих в плоскости ZOX строятся эпюры изгибающего момента М_у и поперечной силы Q_z, а для сил, лежащих в плоскости YOX эпюры М_z и Q_у. Наконец, для моментов лежащих в плоскостях, перпендикулярных к оси ОХ, строится эпюра крутящих моментов М_к= М_х. Если среди внешних сил имеются продольные силы, то дополнительно для них должна быть построена эпюра продольных сил N=P_x. На основании построенных эпюр можно проверить прочность в любом сечении вала.

Изгибающие моменты М_у и М_z и поперечные силы Q_y и Q_z можно сложить:

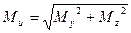
В результате применения этих формул могут быть построены эпюры М_u и Q. При их построении надо иметь в виду следующее.

1. Суммарная поперечная сила Q может не менять в плоскости действия суммарного изгибающего момента М_u, и поэтому между ними не будет уже не будет соблюдатся зависимости

2. Эпюра суммарного изгибающего момента М_u будет изображаться прямой линией на тех участках, на которых эпюры М_z и М_y также изображаются прямыми линиями с общей нулевой точкой.

3. На тех участках, где М_y и М_z изображаются прямыми линиями, но имеют нулевые точки в разных сечениях эпюра М_u будет изображаться вогнутой кривой, то есть будет иметь наибольшую ординату на одном из концов участка, и строится по точкам.

В конечном итоге для круглого вала в произвольном сечении могут действовать четыре силовых фактора: продольная сила, изгибающий момент М_u, поперечная сила Q и крутящий момент М_к. Необходимо рассчитать прочность данного сечения, имеющего диаметр d.

Продольная сила вызывает в сечении равномерно распределенные нормальные напряжения: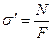

Максимальные напряжения от изгибающего момента имеют место в двух диаметрально противоположных точках контура и по величине равны:

Очевидно, что в одной из этих двух точках напряжения и одинаковы по знаку, поэтому абсолютная величина суммарного нормального напряжения в одной из этих точек (1)

Здесь N и М_u взяты по их абсолютной величине.

Крутящий момент М_к вызывает наибольшие касательные напряжения во всех точках контура сечения:

Наибольшие касательные напряжения от сдвига, вызываемого поперечной силой, будут существовать в двух диаметрально противоположных точках контура и по величине равны

В одной из этих точек контура напряжения и будут иметь одинаковое направление и сложатся арифметически:

(2)

Делая некоторую небольшую ошибку в запас прочности, принимаем, что точка с наибольшим нормальным и касательным напряжением совпадают.

Чтобы упростить расчетные формулы для наиболее часто встречающего случая расчета стержня круглого сечения, формулы (1) и (2) полезно несколько преобразовать. Первую из них можно переписать так:

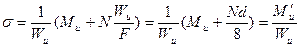(3)

где 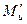- приведенный изгибающий момент, эквивалентный по величине вызываемого им максимального нормального напряжения одновременному действию реальных силовых факторов μ_u и N: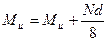

Аналогично формула (2) принимает вид:

где - приведенный крутящий момент, эквивалентный по величине вызываемого или максимального касательного напряжения действительным силовым факторам М_к и Q:

Теперь, применяя различные теории прочности для проверки круглого вала на совместное действие изгиба и кручения по напряжениям, можно получить следующие формулы:

По третьей теории (4)

По третьей теории с поправкой Мора:

(5), где

По четвертой теории (энергии формоизменения) (6)

Все формулы можно объединить одним общим выражением:

(7),

где М_u.э. – эквивалентный изгибающий момент по соответствующей теории прочности, равный численно дроби формул.

Для опасного сечения формула (7) преобразуется подстановкой к виду и отсюда находится минимальное необходимое значение d. Оно округляется по ГОСТ до ближайшего размера d, и для этого размера в опасном сечении заново вычисляется значение М_uе с учетом влияния продольной и поперечной сил и проверяется прочность по формуле (7). При этом допускается перенапряжение не свыше 5%.

Понятие об усталости и выносливости материалов

Многие детали машин и механизмов в процессе эксплуатации подвергаются действию циклических переменных нагрузок, то есть таких, которые многократно через определенные интервалы времени приобретают первоначальное значение. Практика эксплуатации машин показала, что под действием циклически меняющихся напряжений материал разрушается при более низких напряжениях, чем при действии постоянных во времени нагрузок. Это явление преждевременного разрушения материала под действием циклически изменяющихся нагрузок получило в технике название усталости материалов, а способность материала противодействовать действию переменных нагрузок называется выносливостью.

Введем отношение 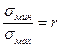,взятое с его алгебраическим знаком, где 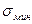- наименьшее напряжение, а - наибольшее напряжение цикла. Под циклом понимается замкнутая однократная смена напряжений, получающих непрерывный ряд значений. Отношение r называется коэффициентом асимметрии.

Если r = -1, цикл называется симметричным. Этот вид нагружения является наиболее опасным.

Опытами установлено, что под действием циклических напряжений с определенным коэффициентом асимметрии материал может разрушиться при верхнем пределе цикла, значительно меньшем не только временного сопротивления материала, но даже и предела текучести, если число перемен нагрузки будет достаточно велико.

Однако для многих материалов и в том числе для всех марок сталей установлено существование предела выносливости (или предела усталости), под которым понимается то наибольшее значение верхнего предела цикла при заданном коэффициенте асимметрии, при котором материал не разрушается при любом числе перемен нагрузки.

Для черных металлов на основе накопленного опыта принято считать, что если образец не разрушается при 10⁷ перемен нагрузки, то он сможет выдержать любое число перемен. Для цветных металлов и сплавов и сплавов принимают за предел выносливости верхний предел цикла, соответствующий числу перемен нагрузки 10⁸ Предел выносливости при симметричном цикле обозначается . Расчет на выносливость проводят, подставляя в ранее приводимые формулы значение вместо .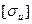

Дата добавления: 2014-01-07