Параллельные подсостояния. Параллельные подсостояния (concurrent substates) позволяют специфицировать два и более подавтомата, которые могут выполняться параллельно внутри составного

Параллельные подсостояния (concurrent substates) позволяют специфицировать два и более подавтомата, которые могут выполняться параллельно внутри составного события. Каждый из подавтоматов занимает некоторую область (регион) внутри составного состояния, которая отделяется от остальных горизонтальной пунктирной линией. Если на диаграмме состояний имеется составное состояние с вложенными параллельными подсостояниями, то объект может одновременно находиться в каждом из этих подсостояний.

Однако отдельные параллельные подсостояния могут, в свою очередь, состоять из нескольких последовательных подсостояний (подавтоматы 1 и 2 на рис. 77). В этом случае по определению объект может находиться только в одном из последовательных подсостояний подавтомата. Таким образом, для абстрактного примера (рис. 6.8) допустимо одновременное нахождение объекта в подсостояниях (1, 3, 4), (2, 3, 4), (1, 3, 5), (2, 3, 5). Недопустимо нахождение объекта одновременно в подсостояниях (1, 2,3) или (3, 4, 5).

Рисунок 77. Графическое изображение составного состояния с вложенными параллельными подсостояниями

Поскольку каждый регион вложенного состояния специфицирует некоторый подавтомат, то для каждого из вложенных подавтоматов могут быть определены собственные начальное и конечные подсостояния (рис. 77). При переходе в данное составное состояние каждый из подавтоматов оказывается в своем начальном подсостояний. Далее происходит параллельное выполнение каждого из этих подавтоматов, причем выход из составного состояния будет возможен лишь в том случае, когда все подавтоматы будут находиться в своих конечных подсостояниях.

Если какой-либо из подавтоматов пришел в свое конечное состояние раньше других, то он должен ожидать, пока и другие подавтоматы не придут в свои конечные состояния.

В некоторых случаях бывает желательно скрыть внутреннюю структуру составного состояния. Например, отдельный подавтомат, специфицирующий составное состояние, может быть настолько большим по масштабу, что его визуализация затруднит общее представление диаграммы состояний. В подобной ситуации допускается не раскрывать на исходной диаграмме состояний данное составное состояние, а указать в правом нижнем углу специальный символ-пиктограмму (рис. 78). В последующем диаграмма состояний для соответствующего подавтомата может быть изображена отдельно от основной с необходимыми комментариями.

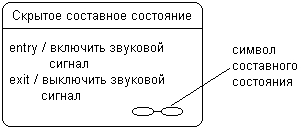
Рисунок 78. Составное состояние со скрытой внутренней структурой и специальной пиктограммой

Дата добавления: 2014-01-07