Случайные погрешности. Вероятностное описание результатов и погрешностей

Когда при проведении с одинаковой тщательностью и в одинаковых условиях повторных наблюдений одной и той же постоянной величины получаем результаты, отличающиеся друг от друга, это свидетельствует о наличии в них случайных погрешностей.

В этом случае предсказать результат отдельного наблюдения и исправить его введением поправки невозможно.

Можно лишь с определенной долей уверенности утверждать, что истинное значение измеряемой величины находится в пределах разброса результатов наблюдений от x_min до x_max, где x_min и x_max - соответственно нижняя и верхняя границы разброса.

Однако остается неясным, какое из множества лежащих в этой области значений величины принять за результат измерения и какими показателями охарактеризовать случайную погрешность результата.

Установить вероятностные (статистические) закономерности появления случайных погрешностей и на основании этих закономерностей дать количественные оценки результата измерения и его случайной погрешности позволяют методы теории вероятностей и математической статистики.

Для характеристики свойств случайной величины в теории вероятностей используют понятие закона распределения вероятностей случайной величины.

Различают две формы описания закона распределения: интегральную и дифференциальную.

В метрологии преимущественно используется дифференциальная форма - закон распределения плотности вероятностей случайно величины.

Если известен дифференциальный закон распределения случайной величины f(x), то вероятность Р её попадания в интервал от х₁ до х₂

Для описания частных свойств случайной величины используют числовые характеристики распределений.

В качестве числовых характеристик выступают моменты случайных величин: начальные и центральные.

Все они представляют собой некоторые средние значения; причём если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра закона распределения - то центральными.

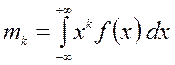Начальный момент k-го порядка определяется формулой

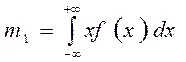Для начальных моментов наибольший интерес представляет математическое ожидание случайной величины (k = 1):

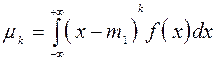Центральные моменты k-го порядка рассчитываются по формулам:

Из центральных моментов особенно важную роль играет второй момент (k = 2) - дисперсия случайной величины D:

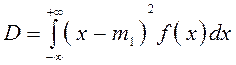Дисперсия случайной величины характеризует рассеяние отдельных её значений. Дисперсия имеет размерность квадрата случайной величины и выражает как бы мощность рассеяния относительно постоянной составляющей.

Однако чаще пользуются положительным корнем квадратным из дисперсии - средним квадратическим отклонением (СКО), которое имеет размерность самой случайной величины.

Дата добавления: 2014-01-07