
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 2 Земные геоцентрические системы координат
|
|
|
|
II. Классификация систем координат.
Необходимость использования различных систем координат в спутниковой геодезии становится понятной, если учесть, что для вычисления орбит спутников, прогнозирования их движения используются одни системы координат, для определения координат пунктов в процессе наблюдения используются другие координаты, а для использования полученных координат при решении различных прикладных задач требуются совершенно иные системы. Кроме того, нужна соответствующая теория времени, поскольку решение задач спутниковой геодезии производится по наблюдениям объектов, часто движущихся с огромными скоростями.
Инерциальными системами координат называют системы, оси которых фиксированы в пространстве, либо изменяющие своё положение с течением времени по хорошо известным законам относительно других фиксированных осей. Свободная материальная точка в такой системе движется равномерно и прямолинейно. Эти системы лучше всего подходят для изучения движения искусственных спутников Земля (ИСЗ).
Системы координат, вращающиеся вместе с Землёй, называют земными.
Инерциальные системы, не участвующие в суточном вращении Земли называют небесными или звёздными.
Системы, начало которых совпадает с центром масс Земли, называют геоцентрическими.
Земные геоцентрические системы называют также общеземными или глобальными, мировыми референцными (опорными), или условными земными (условными – в смысле принятыми по соглашению).
Общеземные системы образуются с помощью методов космической геодезии:
- По наблюдениям на радиоинтерферометрах со сверхдлинными базами.
- Лазерной локацией спутников и Луны.
- По навигационным спутникам.
Квазигеоцентрические, или локальные референцные – системы начало которых находится в центре референц-эллипсоида, наилучшим образом подходящего к территории страны или материка.
Локальные референцные системы образуются с помощью градусных измерений классической геодезии:
- Триангуляции.
- Трилатерации.
- Полигонометрии.
- Астрономических определений.
Топоцентрические – координаты с началом в точке наблюдений. Используются для наблюдений за спутниками относительно точек горизонта или относительно звёзд.
При рассмотрении некоторых вопросов космической геодезии применяются системы координат:
- Гелиоцентрические – с началом в центре Солнца.
- Барицентрические – с началом в барицентре Солнечной системы или барицентра системы «Земля –Луна».
- Планетоцентрические – с началом в центре масс некоторой планеты.
- Спутникоцентрические – с началом в центре масс спутника.
За основную координатную плоскость системы принимают плоскости земного или небесного экваторов, горизонта или орбиты ИСЗ, в связи с чем выделяют:
- Экваториальные системы координат.
- Горизонтальные системы координат.
- Орбитальные системы координат.
Иногда используются:
- Эклиптические системы координат.
- Галактические системы координат.
Направление осей системы координат задаётся относительно некоторых точек небесной сферы или земной поверхности, а также фундаментальных векторов. К этим векторам относят вектор кинетического момента Земли, направление мгновенной оси её вращения, вектор направления силы тяжести, нормаль к орбите Земли (к эклиптике), вектор линии узлов земной орбиты (направление на точку весеннего равноденствия) и другие. Координаты, связанные с отвесной линией, называют астрономическими.
Вследствие того, что выбранные для ориентировки систем точки могут изменять своё положение, обязательно указывается эпоха – тот момент, к которому относятся направление осей. При построении систем координат, в которых учитываются релятивистские эффекты, вводят систему отсчёта и системы времени.
При проведении топографо-геодезических работ и навигации часто используются плоские координаты в различных картографических проекциях. На Украине и в странах СНГ широко распространена проекция Гаусса-Крюгера. В спутниковой аппаратуре и её программном обеспечении пользователи часто встречаются с близкой к ней поперечной проекцией Меркатора UTM.
III. Небесные системы координат.
Для описания движения спутника вокруг Земли в соответствии с законами Ньютона, необходима инерциальная координатная система, в которой можно выражать векторы силы ускорения, скорости и положения. Инерциальная опорная система по определению должна быть стационарной в пространстве или движущейся с постоянной скоростью (без ускорения). Такая система задаётся следующим образом:
-  Начало находится в центре масс Земли О.
Начало находится в центре масс Земли О.
- Ось 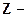 направлена по мгновенной оси вращения Земли к истинному северному полюсу мира Р.
направлена по мгновенной оси вращения Земли к истинному северному полюсу мира Р.
- Ось 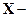 в экваториальной плоскости к истинной точке весеннего равноденствия
в экваториальной плоскости к истинной точке весеннего равноденствия 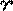 (точке пересечения плоскости истинного экватора Земли с орбитой Земли, наклонённой к экватору на угол
(точке пересечения плоскости истинного экватора Земли с орбитой Земли, наклонённой к экватору на угол 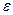 ).
).
- Ось У дополняет систему до правой.
Строго говоря, такая система не отвечает требованиям к инерциальной системе, так как центр масс Земли движется вокруг Солнца с изменяющейся по законам Кеплера скоростью. Однако на коротких интервалах времени такую систему координат можно считать инерциальной.
Положение объекта 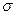 в небесной системе можно задать либо сферическими координатами – прямым восхождением
в небесной системе можно задать либо сферическими координатами – прямым восхождением 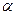 и склонением
и склонением 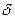 , либо прямоугольными координатами
, либо прямоугольными координатами 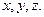 Прямоугольные координаты являются компонентами вектора положения
Прямоугольные координаты являются компонентами вектора положения 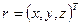 .
.
Прямое восхождение 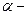 это угол в экваториальной плоскости, измеренный против часовой стрелки от точки весеннего равноденствия до круга склонений (иногда называемого часовым кругом).
это угол в экваториальной плоскости, измеренный против часовой стрелки от точки весеннего равноденствия до круга склонений (иногда называемого часовым кругом).
Склонение объекта 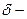 это угол, измеряемый от плоскости экватора до светила; он положителен для объектов в северной полусфере и отрицателен для южной полусферы. При заданном положении спутника в этой системе вводится геоцентрическое расстояние
это угол, измеряемый от плоскости экватора до светила; он положителен для объектов в северной полусфере и отрицателен для южной полусферы. При заданном положении спутника в этой системе вводится геоцентрическое расстояние 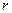 , для звёзд его обычно принимают равным единице.
, для звёзд его обычно принимают равным единице.
Прямоугольные и сферические координаты связаны соотношениями:
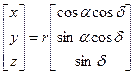 ;
;
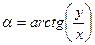 ;
;
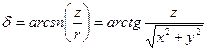 ;
;
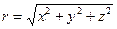 .
.
Описанная система называется истинной небесной системой координат. Основной плоскостью в ней является плоскость истинного небесного экватора, в каждый момент времени совпадающая и плоскостью мгновенного экватора Земли.
Истинная небесная система не является строго инерциальной (по этой причине её иногда называют квазиинерциальной): ориентировка её осей изменяется со временем в пространстве из-за лунно-солнечной прецессии и астрономической нутации земной оси; при этом истинный полюс Р совершает вековое и колебательное движение вокруг полюса эклиптики Рэ . Положение эклиптики в пространстве также изменяется под влиянием прецессии от планет.
IV. Прецессия и нутация.
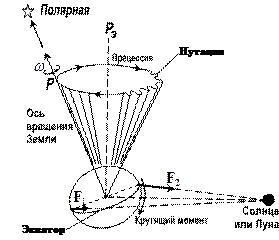 Причина прецессии и нутации лежит в постоянно изменяющемся гравитационном притяжении Солнца, Луны (а так же в малой степени – планет) и элементов масс Земли. Это происходит вследствие орбитального движения Земли и Луны. Поскольку эти изменения в расстояниях являются периодическими, то прецессия и нутация оказываются периодическими функциями времени, что является отражением периодичности орбитальных движений Солнца и Луны; единственное исключение – прецессия от планет.
Причина прецессии и нутации лежит в постоянно изменяющемся гравитационном притяжении Солнца, Луны (а так же в малой степени – планет) и элементов масс Земли. Это происходит вследствие орбитального движения Земли и Луны. Поскольку эти изменения в расстояниях являются периодическими, то прецессия и нутация оказываются периодическими функциями времени, что является отражением периодичности орбитальных движений Солнца и Луны; единственное исключение – прецессия от планет.
 Гравитационное притяжение несферической Земли Солнцем и Луной заставляет Землю колебаться подобно волчку (период около 25700 лет) и при этом испытывать малые наклоны, называемые нутацией (главный период18,6 года). Для точного вычисления прецессии и нутации очень важным является распределение земных масс. Самые важные члены прецессии и нутации зависят от сжатия Земли и несовпадения плоскостей экватора и эклиптики (и несовпадение экваториальной плоскости Луны с эклиптикой). Сферическая Земля с однородным распределением плотности не имела бы ни прецессии, ни нутации.
Гравитационное притяжение несферической Земли Солнцем и Луной заставляет Землю колебаться подобно волчку (период около 25700 лет) и при этом испытывать малые наклоны, называемые нутацией (главный период18,6 года). Для точного вычисления прецессии и нутации очень важным является распределение земных масс. Самые важные члены прецессии и нутации зависят от сжатия Земли и несовпадения плоскостей экватора и эклиптики (и несовпадение экваториальной плоскости Луны с эклиптикой). Сферическая Земля с однородным распределением плотности не имела бы ни прецессии, ни нутации.
Если в положении истинного полюса Р учесть влияние нутации в данную эпоху  , то получится положение среднего полюса
, то получится положение среднего полюса 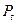 на эту эпоху. Ему соответствует плоскость среднего небесного экватора и средняя точка весеннего равноденствия
на эту эпоху. Ему соответствует плоскость среднего небесного экватора и средняя точка весеннего равноденствия
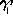 . Такая система называется средней небесной системой в эпоху
. Такая система называется средней небесной системой в эпоху  , а соответствующее положение объекта называют средним положением.
, а соответствующее положение объекта называют средним положением.
Положение основной плоскости и направления координатных осей в пространстве для некоторых эпох Т, называют фундаментальными эпохами и задаваемых обычно на начало Бесселева года, например, В1950.0, или на начало Юлианского года, например, 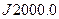 , закрепляются в каталогах координатами
, закрепляются в каталогах координатами 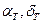 звёзд или других небесных объектов. Связь между средними координатами
звёзд или других небесных объектов. Связь между средними координатами 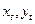 и
и 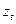 на эпоху наблюдений
на эпоху наблюдений  и средними координатами
и средними координатами 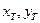 и
и 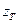 фундаментальной эпохи Т осуществляется с помощью прецессионных параметров
фундаментальной эпохи Т осуществляется с помощью прецессионных параметров 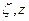 и
и 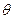 .
.
 На рисунке показаны средние небесные системы координат на эпохи Т и
На рисунке показаны средние небесные системы координат на эпохи Т и  . Экваторы систем отмечены соответственно
. Экваторы систем отмечены соответственно 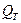 и
и 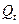 , содержат точки весеннего равноденствия
, содержат точки весеннего равноденствия 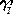 и
и 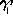 и пересекаются по прямой ОМ. Переход от средней небесной системы эпохи каталога Т к эпохе наблюдений
и пересекаются по прямой ОМ. Переход от средней небесной системы эпохи каталога Т к эпохе наблюдений  через прямоугольные координаты выполняется по формуле:
через прямоугольные координаты выполняется по формуле:
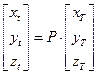 ,
,
в которой Р – матрица для учёта прецессии за интервал времени 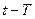 , она вычисляется через экваториальные прецессионные параметры
, она вычисляется через экваториальные прецессионные параметры 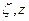 и
и 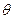 :
:
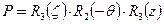
или после перемножения матриц получается как
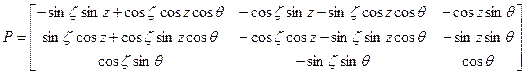
В модели прецессии, принятой Международным астрономическим союзом в 1976 году эти параметры вычисляются по формулам:
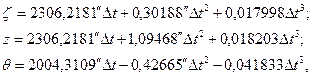
где 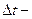 интервал, измеренный в юлианских столетиях по барицентрическому динамическому времени (TDB) между фундаментальной эпохой
интервал, измеренный в юлианских столетиях по барицентрическому динамическому времени (TDB) между фундаментальной эпохой 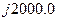 и эпохой
и эпохой 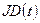 :
:
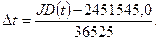
Значение юлианской даты 2451545,0 соответствует эпохе 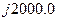 .
.
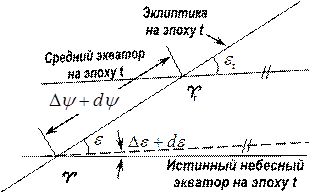 Истинный небесный экватор ортогонален оси вращения Земли и подвержен действию прецессии и нутации, то есть он не совпадает со средним экватором из-за нутации, вычисляемой на нужную эпоху
Истинный небесный экватор ортогонален оси вращения Земли и подвержен действию прецессии и нутации, то есть он не совпадает со средним экватором из-за нутации, вычисляемой на нужную эпоху 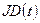 . Нутация раскладывается на долго- и короткопериодическую (период менее 35 суток) нутацию по долготе
. Нутация раскладывается на долго- и короткопериодическую (период менее 35 суток) нутацию по долготе 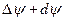 (вдоль эклиптики) и на долго- и короткопериодическую нутацию наклона
(вдоль эклиптики) и на долго- и короткопериодическую нутацию наклона 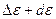 (перпендикулярно эклиптике).
(перпендикулярно эклиптике).
На рисунке показаны средний и истинный экваторы на эпоху  , а также средний наклон эклиптики к экватору
, а также средний наклон эклиптики к экватору 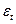 и истинный наклон
и истинный наклон 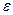 , они связаны через нутация наклона
, они связаны через нутация наклона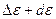 .
.
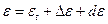
Переход от средних координат в эпоху  к истинным координатам этой же эпохи выполняется через матрицу нутации
к истинным координатам этой же эпохи выполняется через матрицу нутации 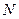 :
:
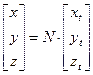
Матрица нутации 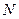 вычисляется через долго- и короткопериодическую нутацию по долготе
вычисляется через долго- и короткопериодическую нутацию по долготе 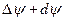 , коротко- и долгопериодическую нутацию наклона
, коротко- и долгопериодическую нутацию наклона 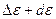 и наклоны эклиптики средний
и наклоны эклиптики средний 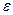 и истинный
и истинный 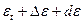 :
:
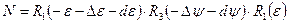 .
.
При разложении с точностью до членов первого порядка формула принимает вид:
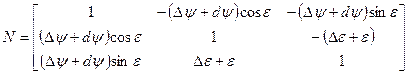
Средний наклон эклиптики к экватору, изменяющийся только под действием прецессии даётся уравнением:
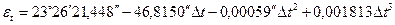 .
.
Полное преобразование от среднего положения в юлианскую дату 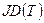 фундаментальной эпохи Т до истинного положения в юлианскую дату
фундаментальной эпохи Т до истинного положения в юлианскую дату 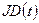 имеет вид:
имеет вид:
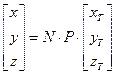
Истинное прямое восхождение 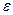 и истинное склонение
и истинное склонение 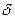 можно вычислить из уравнений:
можно вычислить из уравнений:
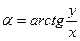 и
и 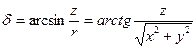 ,
,
Расстояние 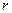 при этом преобразовании не изменяется.
при этом преобразовании не изменяется.
Полный набор членов нутации зависит от принятой модели. В модели нутации МАС от 1980 г., основанной на теории твёрдой Земли Киношита и геофизической модели Джильберта и Дзевонски (твёрдое внутреннее ядро, жидкое внешнее ядро и распределение эластичных параметров, выведенных по большому набору сейсмологических данных), 106 членов. В модели нутации 1996 г. содержится 263 члена по каждому компоненту [IERS,1996], а в моделях МАС 2000А и 2000В содержится 678 членов лунно-солнечной нутации и добавляется 687 членов планетарной нутации [IERS,2003]. Увеличение числа членов объясняется повышением требований к точности координатных преобразований. Первые члены в нутации равны 17,2″ по долготе и 9,2″ по наклону. С увеличением номера расположения в ряду амплитудные коэффициенты становятся всё меньше. В моделях нутации МАС 2000 направление на полюс обеспечивается с точностью 0.0000002".
Истинный полюс мира, положение которого устанавливается на основании теории прецессии и нутации, получил название Небесного эфемеридного полюса (НЭП). Референц-ось, проходящая через НЭП, не совпадает с мгновенной осью вращения Земли и вектором кинетического момента и почти не имеет суточных колебаний ни в инерциальной, ни в земной системах. Степень удаления НЭП от истинного небесного полюса зависит от точности принятых моделей прецессии и нутации. Концепция НЭП (а также связанного с ним небесного эфемеридного начала, Гринвичского истинного звёздного времени и ряда других понятий) позволяет делать строгие преобразования с достаточной точностью не обращаясь к истинному полюсу, положение которого в пределах точности Международной небесной системы отсчёта ICRS не обеспечивается. Более того, концепция НЭП позволяет оперативно совершенствовать теорию координатных систем без введения дополнительных понятий и ограничений.
Введение в использование Международным астрономическим союзом Международной небесной системы ICRS с 1 января 1998 г и точность, достигнутая в большинстве современных моделей и наблюдений вращения Земли требуют переопределения Параметров ориентировки Земли (ПОЗ). Во – первых должны быть переопределены параметры прецессии-нутации и Гринвичского звёздного времени, которые в настоящее время определяются системой FK5, чтобы быть согласованными с ICRS. Во-вторых, принятие определения Небесного эфемеридного полюса НЭП должно быть расширено, чтобы соответствовать большинству современных моделей нутации и полярного движения до микросекундной точности, включая суточные и субсуточные компоненты, как и новые методики наблюдений.
В моделях прецессии и нутации МАС 2000 появились суточные и субсуточные члены. Это привело к значительному усложнению теории прецессии-нутации, связи земных и небесных координатных систем. С появление Международной службы вращения Земли (МСВЗ) в 1988 г стало возможным оперативно уточнять вычисляемое на основе теории положения НЭП по наблюдениям. Смещения небесного полюса публикуются МСВЗ в бюллетене А как поправки по долготе 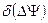 и по наклону
и по наклону 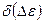 . Это повышает точность привязки небесной системы координат к инерциальному пространству.
. Это повышает точность привязки небесной системы координат к инерциальному пространству.
V. Реализация небесных координат.
Традиционный способ реализации небесной системы координат – составление фундаментальных каталогов звёздных положений, полученных на основе оптических наблюдений ярких звёзд (обычно до 6-7 величины). В частности, с 1986 г в Астрономическом ежегоднике используется схема каталога FK5. Каталог содержит координаты и собственные движения 1535 звёзд для экватора и равноденствия эпохи J2000.0.
Наиболее точные инерциальные небесные системы реализуются МСВЗ в международных небесных систем отсчёта International Celestial Reference Frame, ICRF. Их первая реализация относится к 1995 году. Эти системы определяются через каталоги экваториальных форме координат более чем 200 компактных внегалактических объектов (преимущественно квазаров), полученных по наблюдениях на радиоинтерферометрах со сверхдлинными базами (РСДБ). Объекты в каталоге ICRF разделены на три категории: «определяющие», «кандидаты в определяющие» и «другие». Определяющие источники должны иметь большое число наблюдений (не менее 20), а протяжённость наблюдений должна быть не менее двух лет. Координаты радиоисточников вычисляются ежегодно несколькими Центрами анализа МСВЗ и независимыми группами обработки данных РСДБ. По результатам этой обработки выводятся средние взвешенные координаты источников. Постоянство направлений осей ICRF в пространстве основано на предположении, что внегалактические объекты не имеют никаких собственных движений. Направление осей в ICRF согласованы с системой FK5. Успешные реализации ICRF, сделанные до настоящего времени поддерживают направления осей в пространстве в пределах ±0.00002″.
Для согласования оптической и внегалактической систем отсчёта по рекомендации МАС европейским космическим агентством в августе 1989 г был запущен астрометрический спутник «Гиппаркос». В каталоге Hipparcos приводятся координаты 118218 звёзд на эпоху 1991.25 с их собственными движениями, параллаксами и звёздными величинами.
Каталог фундаментальных звёзд FK6 объединяет наземные астрометрические данные основных фундаментальных звёзд, полученных более чем за два столетия и представляемых в каталоге FK5, с наблюдениями астрометрического спутника Hipparcos. Первая часть каталога FK6 была опубликована в 1999 году.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 9314; Нарушение авторских прав?; Мы поможем в написании вашей работы!