Цилиндрические и конические фигуры

ФИГУРЫ ВРАЩЕНИЯ.

Оборотные средства предприятия

Основные фонды предприятия

Основные фонды - совокупность материально вещественных ценностей, которые используются в течении длительного времени, постепенно изнашиваясь и принося свою стоимость на продукцию по частям в форме армотизационных отчислений.

Состав основных фондов - здания, сооружения, машины и оборудования, транспортные средства, инструменты, инвентарь, капитальные затраты на улучшение земель.

К активной части относят - машины, оборудование, транспортные средства.

К пассивной части относят - здания.

Пути использования основных средств- увеличение доли активной части основных фондов до оптимальной величины, внедрение новой высокопроизводительной, автоматизированной техники, увеличение времени использования оборудования (уменьшение простоев), совершенствование организации производства и труда, планирование, организация рабочего места, повышение квалификации, улучшение работы и труда).

Оборотные средства предприятия - это сумма его оборотных фондов и фондов обращения, которые используются в течении одного цикла, полностью перенося свою стоимость на продукцию или услуги.

Состав основных фондов - сырье и материалы, запчасти для ремонта, полуфабрикаты, топливо, незавершенное производство, расходы будущих периодов, готовая продукция на складах, готовая продукция (отгруженная), но не оплаченная, дебиторская задолженность.

Оборотные средства находятся в постоянном движении.

Пути эффективного использования оборотных средств- внедрение экономически обоснованных норм запаса ОС, с учетом внедрения НТП, современная организация складского хозяйства и учета сырья и материалов, своевременное заключение договоров на поставку сырья, материалов и вывоз готовой продукции, активизация маркетинговой деятельности, увеличение объема и роста коэффициента оборачиваемости.

В этом параграфе мы рассмотрим некоторые часто встречающиеся типы пространственных фигур и приведем примеры таких фигур, которые задаются уравнениями второй степени, т.е. являются, фигурами второго порядка в пространстве.

п.1. Фигуры вращения

Пусть – прямоугольная система координат в пространстве 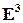, – фигура на координатной плоскости 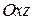(рис. 1), заданная общим уравнением

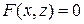. (1)

Обозначим фигуру в пространстве, которая получается вращением плоской фигуры вокруг оси (рис. 2).

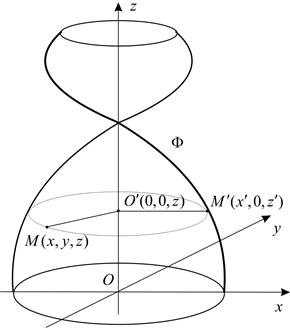
Рис.1 Рис.2

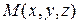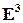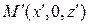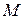Зная уравнение (1) фигуры , можно получить уравнение фигуры . Точка пространства тогда и только тогда принадлежит фигуре , когда она получена вращением вокруг оси некоторой точки фигуры (рис. 2). Поскольку и 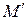лежат в одной плоскости, параллельной плоскости 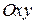, то 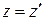. Кроме того, поскольку 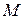и 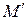лежат на одной окружности с центром в точке 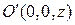и радиуса , то 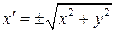. Таким образом,

.

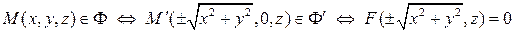Следовательно, уравнение фигуры , полученной вращением вокруг оси плоской фигуры с уравнением (1), имеет вид:

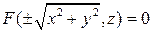. (2)

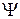Сечение фигуры вращения любой плоскостью, проходящей через ось вращения , есть плоская фигура , симметричная относительно оси вращения, которая называется меридианом фигуры вращения (иногда меридианом называют каждую из двух «половинок» фигуры 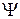, лежащую в одной полуплоскости относительно прямой ). Очевидно, что фигура может быть получена вращением вокруг оси любого своего меридиана и при повороте вокруг оси на любой угол меридианы переходят друг в друга. Сечение фигуры плоскостью, перпендикулярной оси вращения, называется параллелью фигуры вращения . Любая непустая параллель есть объединение концентрических окружностей (возможно, нулевого радиуса). Если математической моделью поверхности земного шара считать сферу (фигуру вращения с осью вращения, проходящей через полюса), то математическая терминология совпадает с географической.

Рассмотрим ряд примеров фигур вращения.

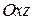1. Пусть – прямая в плоскости с уравнением . Фигура , полученная вращением прямой вокруг оси , называется круговым цилиндром (рис. 3).

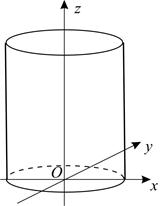
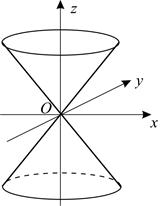
Рис.3 Рис.4

Круговой цилиндр, как показано выше, можно задать уравнением:

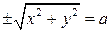или .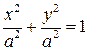

Меридианы кругового цилиндра – это прямые (образующие цилиндра), параллели – окружности радиуса .

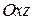2. Пусть – прямая в плоскости с уравнением 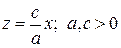. Фигура , полученная вращением прямой вокруг оси , называется круговым конусом второго порядка (рис. 4). Круговой конус второго порядка можно задать уравнением:

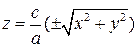или .

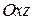3. Пусть – эллипс в плоскости с каноническим уравнением . Фигура , полученная вращением эллипса вокруг оси , называется эллипсоидом вращения (рис. 5).

Рис.5

Эллипсоид вращения можно задать уравнением:

или .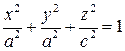

Меридианы эллипсоида вращения – эллипсы, канонические уравнения которых совпадают с уравнением исходного эллипса , параллели – окружности, радиусы которых принимают все значения на отрезке .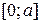

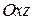4. Пусть – гипербола в плоскости с каноническим уравнением 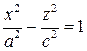. Фигура , полученная вращением гиперболы вокруг ее мнимой оси , называется однополостным гиперболоидом вращения (рис.). Однополостный гиперболоид вращения можно задать уравнением:

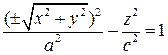или .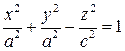

Меридианы однополостного гиперболоида вращения – гиперболы, канонические уравнения которых совпадают с уравнением исходной гиперболы , параллели – окружности, радиусы которых принимают все значения на луче . Параллель наименьшего радиуса , лежащая в плоскости 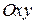, называется горловой окружностью.

5. Пусть – гипербола в плоскости 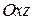, сопряженная гиперболе из предыдущего примера, с каноническим уравнением . Фигура , полученная вращением гиперболы вокруг ее действительной оси , называется двуполостным гиперболоидом вращения (рис.). Двуполостный гиперболоид вращения можно задать уравнением:

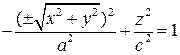или .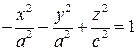

Двуполостный гиперболоид состоит из двух частей («полосте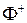й») и 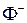, расположенных в разных полупространствах относительно координатной плоскости 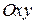. Точк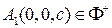и и 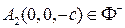называются вершинами гиперболоида. Меридианы двуполостного гиперболоида вращения – гиперболы, канонические уравнения которых совпадают с уравнением исходной гиперболы , параллели – окружности, радиусы которых принимают все значения на луче .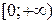

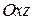6. Пусть – парабола в плоскости с каноническим уравнением 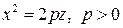. Фигура , полученная вращением параболы вокруг ее оси , называется эллиптическим параболоидом вращения (рис.). Эллиптический параболоид вращения можно задать уравнением:

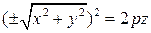или .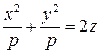

Точка называется вершиной параболоида. Меридианы эллиптического параболоида вращения – параболы, канонические уравнения которых совпадают с уравнением исходной параболы , параллели – окружности, радиусы которых принимают все значения на луче .

п.2. Цилиндрические фигуры

Пусть – фигура, лежащая в плоскости ,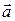– ненулевой вектор, не параллельный плоскости . Рассмотрим всевозможные прямые 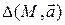с направляющим вектором 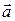, начальные точки которых 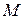пробегают множество . Объединение этих параллельных прямых называется цилиндрической фигурой (рис.). При этом называется базой фигуры , а прямые 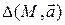– ее образующими. Уравнение цилиндрической фигуры можно получить следующим образом. Выберем аффинную систему координат в пространстве 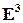так, чтобы координатная плоскость 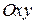совпадала с плоскостью , а ось имела направляющий вектор 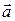. Пусть

(3)

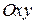– уравнение базы в системе координат . Очевидно, что точка 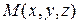пространства 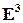принадлежит цилиндрической фигуре тогда и только тогда, когда ее проекция 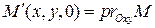на плоскость 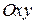параллельно оси принадлежит фигуре . Следовательно, в выбранной системе координат уравнение цилиндрической фигуры имеет вид (3), т.е. совпадает с уравнением базы. Таким образом, уравнение (3) задает базу цилиндрической фигуры , если это уравнение рассматривать относительно системы координат 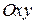на плоскости , и это же уравнение задает цилиндрическую фигуру , если его рассматривать относительно системы координат в пространстве .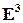

Рассмотрим некоторые примеры цилиндрических фигур. Все уравнения, приведенные ниже, рассматриваются относительно прямоугольной системы координат в пространстве .

1. Пространственная фигура с уравнением

(4)

называется эллиптическим цилиндром (рис.). Базой эллиптического цилиндра является эллипс на плоскости 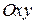с каноническим уравнением (4), образующие цилиндра параллельны оси .

2. Пространственная фигура с уравнением

(5)

называется гиперболическим цилиндром (рис.). Базой гиперболического цилиндра является гипербола на плоскости 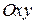с каноническим уравнением (4), образующие цилиндра параллельны оси .

3. Пространственная фигура с уравнением

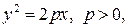(6)

называется параболическим цилиндром (рис.). Базой параболического цилиндра является парабола на плоскости 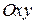с каноническим уравнением (6), образующие цилиндра параллельны оси .

п.3. Конические фигуры

Пусть 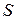– фиксированная точка пространства 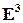. Конической фигурой с вершиной 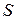называется любое семейство прямых, проходящих через точку 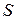(рис.). В качестве примеров таких фигур рассмотрим фигуры, которые задаются уравнениями вида

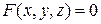, (7)

где 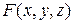– однородная функция степени 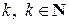, т.е. такая функция трех переменных, для которой выполняется условие:

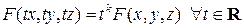. (8)

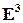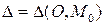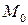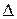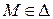Если – аффинная система координат в пространстве то однородное уравнение (7) задает коническую фигуру с вершиной в начале координат либо точку . Действительно, вместе с каждой точкой фигуры этой фигуре принадлежит вся прямая , проходящая через точки и : любая точка прямой имеет вид , и, следовательно , так как 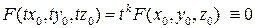. Примером такой фигуры служит круговой конус второго порядка с уравнением , определенный в первом пункте этого параграфа.

Дата добавления: 2014-01-07