Два режима движения жидкости. Число Рейнольдса

2.

F ₁ w ₁ = F ₂ w ₂ = Q = const. (6.3)

Уравнение (6.3) представляет собой уравнение неразрывности потока. Оно показывает, что при установившемся движении через любое сечение потока за единицу времени проходит одно и то же количество жидкости.

На основании уравнения (6.3) можно заключить, что средние скорости потока обратно пропорциональны площадям соответствующих живых сечений:

w ₁ / w ₂ = F ₂ / F ₁. (6.4)

3. Полная удельная энергия потока равна сумме удельной кинетической энергии потока Э _к и удельной потенциальной энергии Э _п:

Э _уд = Э _к + Э _п. (6.5)

Величина, удельной потенциальной; энергии не зависит от положения рассматриваемой точки е (рис. 2.6) и равна:

Э _п = p / (ρ g) + z = const. (6.6)

Подставив значения удельных кинетической и потенциальной энергий, получим выражение для полной удельной энергии потока в выбранном сечении:

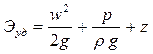. (6.7)

4. При движении реальной жидкости часть энергии затрачивается на преодоление силы трения (сопротивления) на пути от первого сечения ко второму. Эта энергия обращается в тепло и рассеивается. Величину указанных потерь энергии обозначим .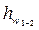

Тогда баланс энергии в сечениях І – І и ІІ – ІІ можно записать в следующем виде:

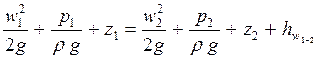. (6.8)

Выражение (6.8) называется уравнением Д. Бернулли. Оно показывает, что за счет

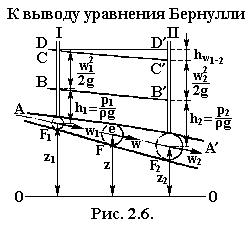преобразования одного вида энергии в другой мы наблюдаем при возрастании скорости уменьшение давления, и наоборот, при уменьшении скорости – возрастание давления. Легко убедиться, что каждый член уравнения Бернулли имеет линейную размерность и может рассматриваться как высота столба жидкости (напор жидкости): α w ² / (2 g) – высота скоростного напора; p / (ρ g) – пьезометрическая высота [может быть измерена в каждом сечении пьезометром (рис. 2.6)]; z – геометрическая высота; 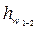– высота потерянного напора, равная части энергии, необратимо превращенной в тепло.

Сумма трех высот: скоростного напора, пьезометрической и геометрической – называется гидродинамическим напором:

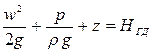(6.9)

Линия 0 – 0 – след плоскости сравнения, линия АА' называется геометрической линий, линия ВВ' называется пьезометрической линией. Линия СС' называется напорной линией. Линия DD' называется линией первоначального напора. Очевидно, отрезок D'C' соответствует потере напора 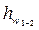на участке между сечениями І – І и ІІ – ІІ:

Уравнение Д. Бернулли являетсяосновным уравнением гидродинамики, в котором в математической форме записан закон сохранения энергии.

Самостоятельная работа студентов

Практическое применение уравнения Бернулли

Уравнение Бернулли имеет большое научное и практическое значение.

На использовании уравнения Бернулли основан также принцип работы многих измерительных приборов. Рассмотрим некоторые из них.

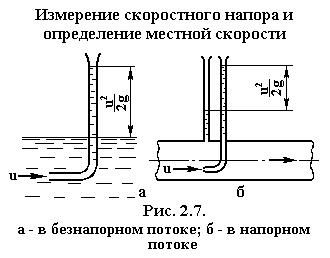
1. Измерение скоростного напора и определение местной скорости потока.

Величина скоростного напора может быть измерена опытным путем, если в поток жидкости поместить против течения на определенной глубине изогнутую под прямым углом трубку, открытую с обеих сторон.

Схема конструкции такой трубки, называемой трубкой Пито, приведена на рис. 2.7,а.

Для измерения скоростного напора в какой-либо точке сечения напорного потока пользуются конструкцией гидродинамической трубки, в которой объединены трубка Пито и пьезометр. Такая конструкция называется трубкой Пито – Прандтля, а ее конструкция схематически показана на рис. 2.7,б.

2. Определение расхода жидкости. Водомер Вентури.

Наиболее простым и точным способом измерения расхода жидкости является объемный способ (рис. 2.8).

В природе существуют два режима движения жидкости: ламинарный (слоистый) и турбулентный (беспорядочный). При ламинарном режиме частицы движутся в виде отдельных, не перемешивающихся между собой, слоев, или струй жидкости. При турбулентном режиме движение частиц беспорядочное, струйчатость потока нарушается, и траектории частиц приобретают сложную форму, пересекаясь между собой.

Английский ученый О. Рейнольдс (1883 г.) опытным путем; подтвердил предположение Д.И. Менделеева и показал также, что при известных условиях возможен переход от одного режима движения к другому и обратно. Подобный опыт можно воспроизвести на установке Рейнольдса (рис. 2.9,а).

При постепенном открытии крана жидкость из сосуда А начинает вытекать; одновременно в поток подается тонкая струйка краски; если она не смешивается с движущейся в трубке Б жидкостью, то это будет означать, что режим движения жидкости ламинарный (рис. 2.9,б).

Постепенно увеличивая открытие крана В и тем самым изменяя скорость течения жидкости в трубе Б, можно наблюдать, как струйка краски начнет колебаться, а затем разрываться и через некоторое время равномерно окрасит всю жидкость в трубке.

Это значит, что ламинарный режим движения перешел в турбулентный (рис. 2.9,в).

безразмерную величину, определяющую режим движения жидкости, которую назвали числом Рейнольдса.

Re = ρ w d / μ = w d / ν. (6.10)

Точными измерениями в круглых гладких трубах установлено, что при Re < 2300 режим движения ламинарный, при Re > 2300 – турбулентный.

Дата добавления: 2014-01-07