Лекция 8

Векторный потенциал, его выражение через плотность тока, теорема Гаусса для индукции магнитного поля. Теорема о циркуляции для индукции магнитного поля. Потенциальные и соленоидальные поля. Элементарный виток с током (магнитный диполь), энергия магнитного диполя во внешнем поля и сила, действующая на магнитный диполь в магнитном поле. Поле магнитного диполя.

Расчеты индукции магнитного поля могут быть значительно упрощены путем введения вспомогательного вектора, который называется векторным потенциалом

(1)

Чтобы оценить полезность введения векторного потенциала, возьмем ротор от выражения (1). Заметим, что дифференцирование при взятии роторы идет по нештрихованным координатам, а интегрирование по штрихованным. Поэтому операцию ротор можно внесте под знак интеграла:

При этом мы использовали формулы векторного анализа

(2)

Итак, индукция магнитного поля выражается через вспомогательный вектор формулой

(3)

Иногда оказывается более удобным вместо прямого использования закона Био-Савара-Лапласа сначала вычислить векторный потенциал, а затем взять от него ротор и получить индукцию магнитного поля.

Полезность векторного потенциала этим не исчерпывается. Он оказывается очень полезным для получения общих теорем относительно свойств индукции магнитного поля. Действительно, взяв дивергенцию от соотношения (3), мы немедленно получаем утверждение (так как дивергенция ротора равна нулю)

(4)

Это утверждение носит название дифференциальной формы теоремы Гаусса для индукции магнитного поля. Получим интегральную форму этого утверждения. Для этого проинтегрируем уравнение (4) по произвольному объему и воспользуемся теоремой Остроградского-Гаусса, которая связывает и нтеграл по объему с интегралом по поверхности этого объема:

(5)

то есть поток индукции по любой замкнутой поверхности равен нулю. Сравним теорему Гаусса для индукции магнитного поля с соответствующей теоремой для напряженности электрического поля

(6)

Это сравнения можно интерпретировать как отсутствие в природе магнитных (смотри замечание в начале лекции 7). Структуру магнитного поля (также и электрического поля)удобно изображать с помощью магнитных силовых линий: кривые, касательные к оторым в каждой точке пространства совпадают снаправлением вектора (обсудить как выбрать одно из двух возможных направлений силовой линии). На языке силовых линий утверждение теоремы Гаусса для магнитного поля сводится к утверждению, что магнитные силовые линии не имеют начала и конца, а являются замкнутыми.

Получим теперь теорему о циркуляции индукции магнитного поля по замкнутому контуру. Для этого вычислим ротор индукции магнитного поля:

(7)

Здесь использована известная формула векторного анализа , и лапласиан равен . Позже мы покажем, что всегда можно положить . Тогда формуы (7,1) дают

(8)

То есть мы получили утверждение

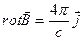(9)

Это утверждение называется дифференциальной формой теоремы о циркуляции для индукции магнитного поля. При этом иы использовали два математических результата

(10)

Первое утверждение может быть проверено непосредственным вычислением (с учетом свойств 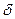- функции). Кроме того, его справедливость можно увидеть из анализа решения для потенциала точечного заряда

(11)

Второе утверждение в (10) является фактически определение обобщенной 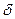- функции. Можно получить и интегральную форму теоремы о циркуляции. Для этого рассмотрим произвольный (достаточно гладкий контур) и поверхность, которая опирается на этот контур

Вычислим поток 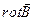через поверхность и воспользуемся теоремой Стокса (поток от ротора вектора преобразуется в циркуляцию вектора):

(12)

Покажите, что правая часть в (12) не зависит от выбора поверхности (при фиксированном контуре).

Доказанные теоремы позволяют дастаточно просто решать задачи с простой геометрией токов. Рассмотрим, например, вычисление индукции для бесконечного прямого провода с током

Индукия направлена по касательной к выбранному круговому контуру радиуса 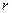и в силу симметрии одинакова для любой точки контура. Отсюда циркуляция равна

(13)

Аналогично рассматриваются другие простые задачи (например, индукция магнитного поля бесконечного соленоида).

Сравним теперь теоремы Гаусса и о циркуляции для электрического и магнитного полей:

(14)

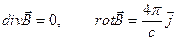(15)

Векторное поле со свойствами (14) (ротор равен нулю) называется потенциальным или безвихревым. Для такого поля циркуляция по любому замкнутому контуру равна нулю, то есть силовые линии не образуют вихрей. Векторное поле со свойствами (15) состоит только из вихрей: оно называется вихревым или соленоидальным.

Рассмотрим некоторую ограниченную область, в которой текут замкнутые токи и вычислим векторный потенциал на больших (много больших, чем размер области) расстояниях. То есть нам надо приближенно вычислить

(16)

Подобную задачу мы решали для электрического потенциала при рассмотрении дипольного приближения. Также как и там используем разложение

(17)

Первый интеграл в (17) равен нулю (разбиваем область на трубки с током, которые замкнуты):

Преобразуем второй интеграл следующим образом

(18)

Довольно трудное, но короткое доказательство приведено в приложении к этой лекции.

Определим магнитный момент области с токами как

(19)

Тогда векторный потенциал на больших расстояних с учетом (18) равен

(20)

Можно вычислить и индукцию

(21)

В чем-то формулы (20,21) напоминают формулы для потенциала и напряженности электрического поля элементарного диполя. Формулу (19) для маленького витка с током можно записать так

(22)

Где площадь витка с током, - ток, 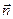- единичный вектор, определяемый по правилу правого винта. Вычислим потенциальную энергию витка с током в постоянном магнитном поле. Рассмотрим процесс образования (растягивания витка от нулевой площади). При перемещении контура с током совершается работа

Это работа силы Ампера, а работа против силы Ампера как раз и равна потенциальной энергии

(23)

Это выражение совпадает с энергией электрического диполя в однородном электрическом поле. Отсюда следует, что и вращающий момент для магнитного диполя должен даваться формулой, аналогичной формуле для электрического диполя

(24)

Приложение.

Симметричная часть дает нуль после перехода к поверхностному интегралу.

Антисимметричная часть дает компоненту двойного векторного произведения

Дата добавления: 2014-01-07