Статистические характеристики системы двух случайных величин. Коэффициент корреляции

Двумерные статистические модели в геологии

Система двух случайных величин имеет пять основных статистических характеристик: средние значения, их дисперсии и их корреляционный момент (или ковариацию) K_ху, которые вычисляют по формулам:

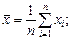
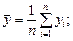(3.1)

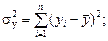(3.2)

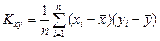. (3.3)

Первые четыре формулы встречались ранее. Особый интерес представляет пятая формула, которая отражает взаимосвязь между случайными величинами х и у. Поскольку корреляционный момент имеет размерность, его преобразуют в безразмерную величину по формуле

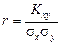. (3.4)

Величина r играет чрезвычайно большую роль в статистических исследованиях и называется коэффициентом корреляции. Его значения заключены в интервале между +1 и –1. Если коэффициент корреляции равен нулю, то линейная связь между случайными величинами отсутствует (рис.3.1, в). При r = 1 связь функциональная положительная (см. рис.3.1, а). При r = –1 связь функциональная отрицательная (см. рис.3.1, б). В реальных условиях коэффициент корреляции не бывает равен единице (или минус единице) и характеризует степень статистической связи между свойствами х и у. Чем ближе по абсолютной величине r к единице, тем сильнее связь между свойствами свойствами; она может быть положительной (r > 0) и отрицательной (r < 0). Таким образом, коэффициент корреляции является мерой линейной зависимости между двумя величинами. Для оценки нелинейных зависимостей он непригоден.

На вычисленную величину r _в заметно влияет случайная погрешность измерений исходных данных, уменьшая истинное значение коэффициента корреляции r:

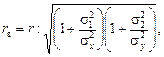(3.5)

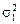где и 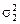– дисперсии случайной погрешности измерений величин х и у соответственно.

Влияние погрешности может оказаться настолько значительным, что зависимость между случайными величинами не будет выявлена.

Статистическая линейная связь между характеристиками двух свойств считается доказанной, если критерий t будет больше предельного t _доп. Коэффициент корреляции, при котором связь считается доказанной, называется значимым коэффициентом корреляции. Для установления значимости используется критерий t, основанный на распределении Стьюдента с числом степеней свободы k = n – 2:

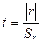при , (3.6)

где S_r – оценка среднеквадратичного отклонения коэффициента корреляции.

Если критерий t будет больше допустимого t _доп при заданной вероятности b, то связь считается доказанной. Имеет смысл принять вероятность b = 0,0027, что соответствует правилу «трех сигм».

При большом значении n можно пользоваться более простым критерием, основанным на нормальном законе распределения:

при . (3.7)

Если t > 3 (что соответствует вероятности b = 0,0027), то связь считается доказанной.

Еще один критерий предложен Фишером:

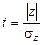при 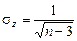, (3.8)

где z – новая переменная, полученная преобразованием коэффициента корреляции через гиперболический арктангенс,

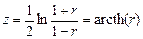. (3.9)

И здесь для доказательства связи необходимо выполнение условия t > 3.

Из соотношения (3.6) выводится формула значимого коэффициента корреляции

. (3.10)

Так как t _доп зависит от числа наблюдений (точнее, от числа степеней свободы k = n – 2), то и значимый коэффициент корреляции зависит от числа наблюдений. При увеличении числа наблюдений, как следует из соотношения (3.7), формула (3.10) упрощается:

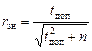. (3.11)

Обычно принимается значение t _доп = 3.

Пример 1. Известны содержания общего и магнетитового железа в руде. Требуется рассчитать коэффициент корреляции между этими величинами (табл.3.1).

Решение:

Таблица 3.1

Дата добавления: 2014-01-07