Построение линии пересечения поверхностей способом секущих плоскостей

Лекция № 14

Построение линии пересечения двух поверхностей в общем случае

Построение линии взаимного пересечения поверхностей заключается в следующем:

- проводят несколько вспомогательных поверхностей, пересекающих данные поверхности;

- строят линии, по которым вспомогательные поверхности пересекают каждую из данных поверхностей;

- находят точки, в которых построенные линии пересекаются между собою;

- соединяют найденные точки в правильной последовательности и получают линию, по которой данные поверхности пересекаются между собою.

В качестве вспомогательных поверхностей – поверхностей-посредн­иков – могут применяться плоскости и кривые поверхности цилиндрические, конические, сферические. Чаще других поверхностями-посредниками являются плоскости частных и общего положений, а также сферические поверхности.

Вспомогательные поверхности подбираются так, чтобы они пересекали данные поверхности по простым для построения линиям – прямым и окружностям.

Приступая к построению линии пересечения, прежде всего, выявляют ее так называемые очевидные, иначе явные точки, то есть точки, которые для своего нахождения не требуют каких-либо построений и усматриваются непосредственно из задания.

В следующую очередь находят особые, характерные, иначе опорные точки линии пересечения. К таким точкам относятся точки, лежащие на очерках проекций данных поверхностей, то есть точки, отделяющие видимую часть линии перехода от невидимой, крайние точки – правая, левая, высшая и низшая, точки – ближайшая к наблюдателю и наиболее удаленная от него.

В последнюю очередь, находят все остальные точки линии пересечения, которые называются промежуточными или случайными. Эти точки определяются в тех участках искомой кривой, где она недостаточно выявлена ранее построенными точками.

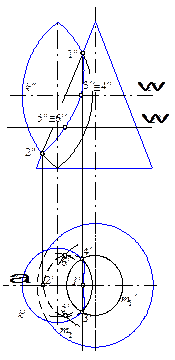
На рис. 14.1 построена линия пересечения двух поверхностей вращения – тора и конуса. Для построения точек этой линии могут быть выбраны только вспомогательные горизонтальные плоскости, расположенные перпендикулярно к осям поверхностей, так как они пересекают их по окружностям.

Рис. 14.1

Характерные точки 1 и 2, расположенные на очерковых линиях фронтального изображения, находятся в плоскости a общей симметрии данных поверхностей. Эта плоскость является фронтальной, поэтому точки 1 и 2 очевидны.

Точки 3 и 4 на экваторе тора найдены с помощью плоскости w₁, которая пересекает тор по экватору k, а коническую поверхность – по окружности m ₁. Горизонтальные проекции линий k и m ₁ пересекаются в точках 3¢ и 4¢. Они, очевидно, расположены на линии, перпендикулярной к плоскости a. Поэтому фронтальные проекции точек 3 и 4 совпадают.

Промежуточные точки 5 и 6 найдены с помощью второй горизонтальной плоскости w₂. Фронтальные проекции точек 5 и 6 также совпадают.

Не вся построенная кривая видна на фронтальной проекции: половина ее находится на задней стороне данных поверхностей, при этом, невидимая ее часть закрывается видимой. На горизонтальной проекции видна часть 3-1-4 кривой, расположенная выше экватора тора (видимость меняется в точках 3 и 4, лежащих на экваторе).

Контрольные вопросы по теме лекции:

1. Назовите алгоритм построения линии пересечения двух поверхностей: общие случаи, частные случаи.

2. В каких случаях при построении линии пересечения двух поверхностей применяется плоскость?

3. Из каких соображений выбирается плоскость-посредник, и какие плоскости целесообразно использовать в качестве вспомогательных плоскостей?

4. В чем состоит упрощение решения задачи по определению линии пересечения поверхностей, если одна (две) из поверхностей является проецирующей?

5. Какие точки линии пересечения поверхностей называются граничными, где они располагаются?

Дата добавления: 2014-01-07