Подстановка

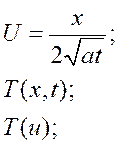
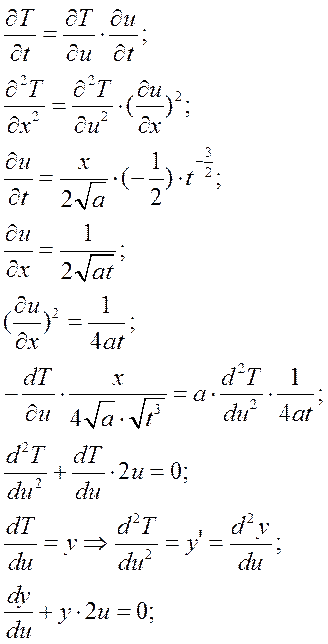
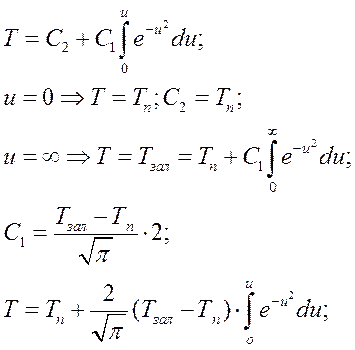
Задача 2

Прогрев полубесконечного тела с граничным условием первого рода

В момент времени t=0, температура на поверхности мгновенно повышается до температуры T_П. Найти зависимость T(x,t).

Запишем уравнение Фурье в форме

Уравнение Фурье:

Начальные условия:

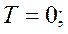
Граничные условия:

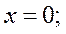
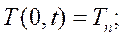
Подстановка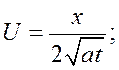

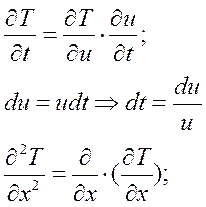
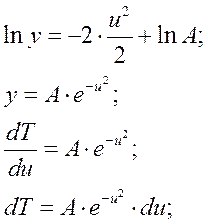
- общее решение

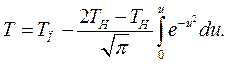- интеграл ошибок Гаусса

Математическая модель затвердевания эвтектических сплавов.

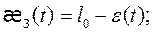
В жидкой фазе:

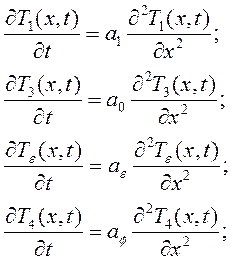
Начальные условия:

Граничные условия:

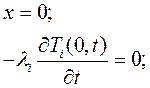i =1,3

Это дифференциальное уравнение затвердевания Стефана

Условно все формы разделяются на 2 группы:

1. песчаные;

2. кокиль.

Песчаные формы:

1. мы не учитываем слой краски (т.к. ее свойства близки к свойствам формы, поэтому мы ей пренебрегаем)

2. прогреваемая:

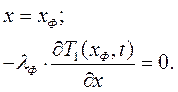
Кокиль:

1. нагреваемая

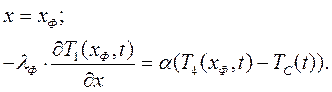
2. толщина кокильной краски много меньше толщины кокиля.

Когда толщина мала, мы можем заменить функцией линейного закона.

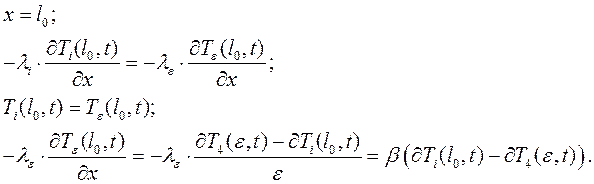
- коэффициент тепловой проводимости кокильной краски.

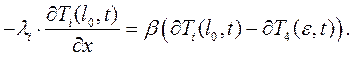
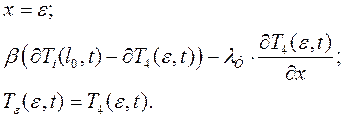
Твердый раствор в кокиле.

Твердый раствор в песчаной форме.

Упрощение математической модели для литья в песчаные формы.

Температура на границе контакта постоянна, следовательно это полубесконечное тело.

На границе 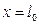- равенство плотности тепловых потоков

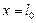
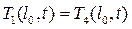
, где

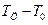- температура перепада по сечению отливки;

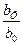- интенсивный фактор;

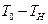- экстенсивный фактор; температурный перепад по сечению формы.

Цель задачи - сравнить температурный перепад.

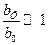, то температурным перепадом по сечению отливки можно пренебречь по сравнению с температурным перепадом по сечению формы.

1 этап- снятие перегрева;

2 этап- затвердевание твердого раствора;

3 этап- затвердевание эвтектики.

Оценка температурного перепада по сечению формы по сравнению с температурным перепадом по сечению отливки.

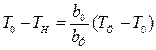
Пренебречь температурным перепадом Т по сечению формы нельзя.

Если 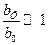, то эта модель весьма малой интенсивности охлаждения.

Упрощение математической модели затвердевания в кокиль.

Т_Ц- температура в центре

Т_П- температура поверхности

Т_К- температура в кокиле на поверхности

Граничные условия:

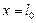, следовательно

Очень приближенно аппроксимируем распределение температур в отливке прямой (----).

Тогда ;

;

;

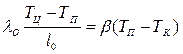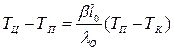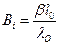- критерий Био

- коэффициент теплопроводности (для Al сплавов ≈100)

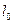- половина толщины (≈5мм)

Следовательно 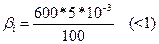- интенсивный фактор;

- температурный напор на границе контакта (экстенсивный фактор).

Температурным перепадом по сечению отливки можно пренебречь по сравнению с температурным напором на границе «отливка-краска».

Для отливки можно использовать модель малой интенсивности охлаждения.

Модель малой интенсивности охлаждения- температура постоянна по сечению, но меняется во времени.

Определение интенсивности нагрева кокиля.

Граничные условия:

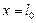, следовательно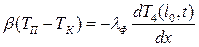

Тогда 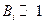, следовательно, для нагрева можно использовать модель малой интенсивности нагрева.

Время цикла- время от окончания заливки до выбивки.

Упрощение дифференциального уравнения теплопроводности Фурье для модели малой интенсивности охлаждения

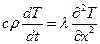. Умножим обе части уравнения на -1 и получим

Принимаем, что 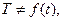следовательно можно записать полную производную:

. Умножим обе части уравнения на dx и получим

q₀ - принимаем равным 0, т.к. T=T_max. В итоге: .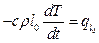

Для кокиля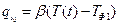

Определение времени снятия перегрева для расплава, залитого в кокиль.

Начальные условия: t=0, T₁(0)=T_ЗАЛ

Граничных условий нет, т.к. температура от границ не зависит!!!

Конечное условие: t₁. Тогда

Температура расплава на границе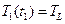

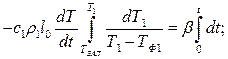
Откуда время снятия перегрева:

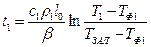
Из уравнения (*):

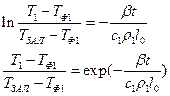
Тогда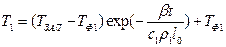

«-»: достаточно сложная формула.

Обычно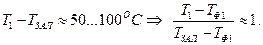

После этого, экспоненту можно разложить в ряд и взять на рассмотрение только 2 первых числа.

Тогда

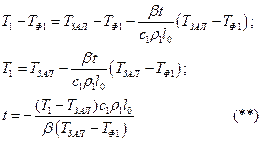
Определение времени снятия перегрева при условии, что температура остается постоянной и начальном условии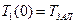

Сравнивая (**) и (***), получаем, что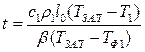

Определение времени снятия перегрева для расплава, залитого в песчаную форму.

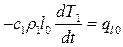
«Отливка-форма»- контакт 2 полубесконечных тел. На границе контакта Т= const поэтому можно взять решение q_l0 из задачи о прогреве полубесконечных тел:

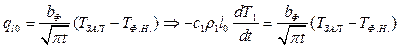
Для песчаной формы более точное значение получается, если брать нижний предел ():

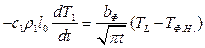
Начальное условие: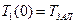

Конечное условие:

ПОЛУЧЕННЫЕ ФОРМУЛЫ СПРАВЕДЛИВЫ ДЛЯ ОТЛИВОК В ФОРМЕ ПЛИТЫ

Для оперирования с отливками любой формы Хворинов ввел понятие приведенного размера:

, где - площадь охлаждаемой поверхности.

Плита:

. Следовательно во всех вышеперечисленных формулах можно заменить: , т.е. мы приводим любую фасонную отливку к плите.

Выбор температуры заливки

При выборе 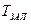следует руководствоваться правилами:

- чтобы в момент окончания заливки расплав не начинал затвердевать;

- при этом мы хотим залить металл с минимальным перегревом.

Расчет потерь перегрева при заполнении расплавом литейной формы

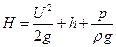- гидравлическая высота;

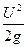- скоростной напор;

h - нивелирная высота;

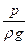- пьезометрическая высота.

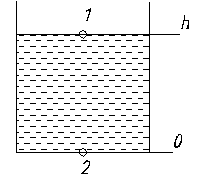Уравнение Бернулли:

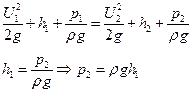, где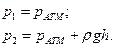

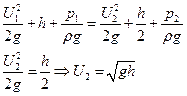
Расчет потерь перегрева при заполнении горизонтального канала кокиля

L- длина кокиля

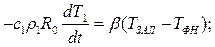
Начальное условие:

- приведенный размер горизонтально канала.

В исходном уравнении температура зависит от времени, а нам нужна зависимость от координаты. Заменим: , где 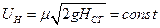, тогда

Начальное условие: z=0, соответственно

Расчет потерь перегрева при заполнении горизонтального канала в песчаную форму

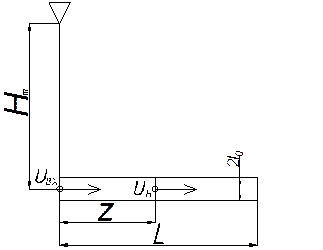
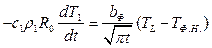
Начальное условие: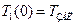

Заменим: , где 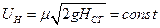, тогда

Расчет потерь перегрева при заполнении вертикального канала кокиля

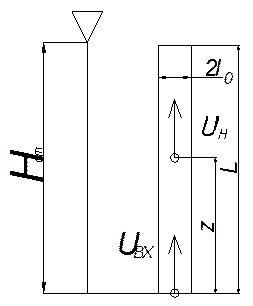
Начальное условие: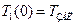

Заменим: , где 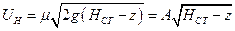, тогда

Домножим на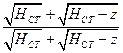

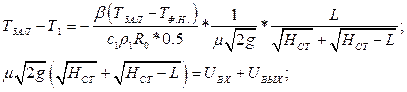
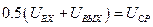- средняя скорость.

Расчет потерь перегрева при заполнении вертикального канала песчаной формы

Начальное условие: 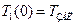Заменим: , где , тогда

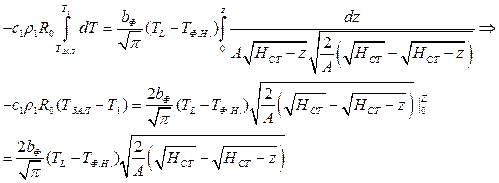
Домножим на сумму корней под корнем:

Расчет потерь перегрева при заполнении наклонного канала кокиля.

Начальное условие: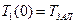

Заменим: , где , тогда

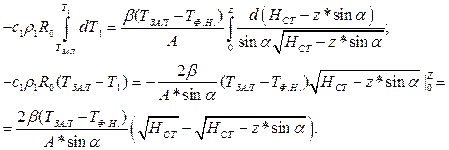
Для вертикального канала 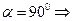формулы совпадают

Для горизонтального канала получаем неопределенность вида по правилу Лопиталя:

Расчет потерь перегрева при заполнении наклонного канала песчаной формы.

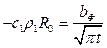
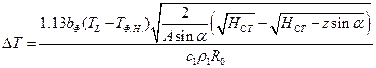
Для вертикального канала 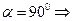формулы совпадают

Для горизонтального канала получаем неопределенность вида по правилу Лопиталя:

Заполнение горизонтального ступенчатого канала при литье в кокиль.

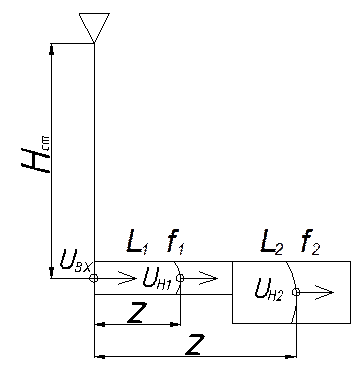
Допущение: каналы заполнены.

Начальное условие:

В исходном уравнении температура зависит от времени, а нам нужна зависимость от координаты. Заменим: , где , тогда

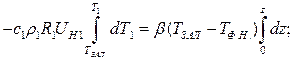
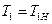- на носике потока

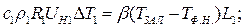
!!!!!- справедлива только для самого узкого канала, а скорости во всех стальных каналах находятся по равенству расходов

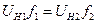
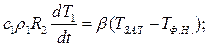
Начальное условие: - момент окончания заполнения первого канала

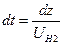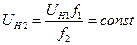Заменим: , тогда

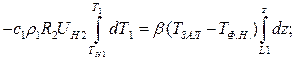
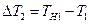- потери перегрева во втором канале.

Переносим начало координат.

!!! При заполнении каналов в кокиле начало координат можно переносить. Результат не изменится.

Вывод: моно переносить начало координат.

Заполнение горизонтального ступенчатого канала при литье в песчаную форму.

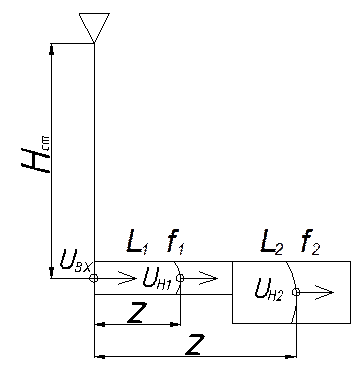
Начальное условие: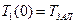

Заменим: , тогда ;

;

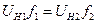где - скорость в вертикальном канале.

Во втором канале:

Начальное условие: 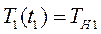- момент окончания заполнения первого канала

Заменим: , тогда ;

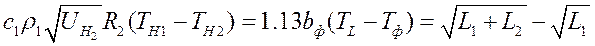
Вывод: нельзя переносить начало координат.

Чем длиннее путь, тем меньше поте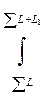ри.

при потери уменьшаются.

Вертикальный канал в кокиле.

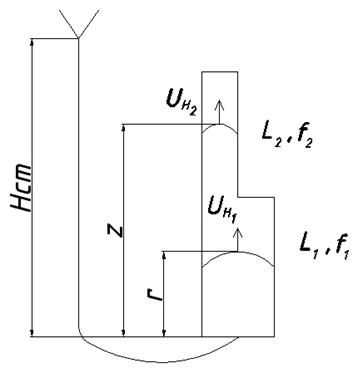
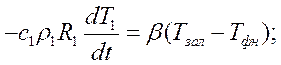
Н.У.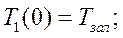

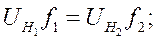
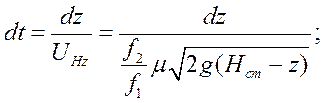
2 канал:

Пределы интегрирования от L₁ до L₁₊ L₂

Вертикальный канал в ПФ.

Н.У.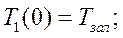

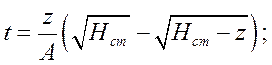
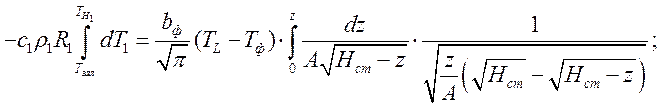
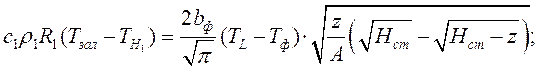
Пределы интегрирования для 2-го канала:

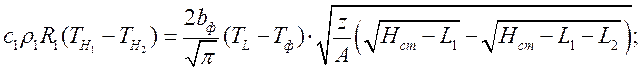
Горизонтальный канал в комбинированной форме.

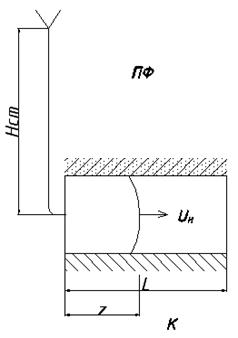
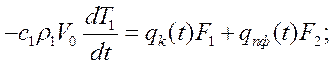
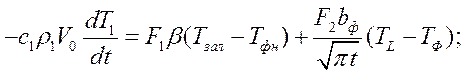
Н.У.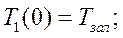

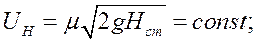
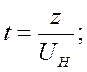
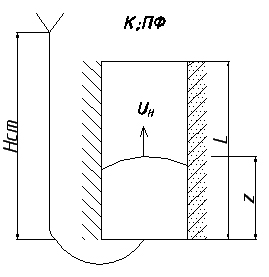
Вертикальный канал в комбинированной форме.

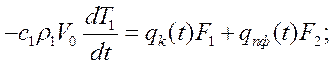
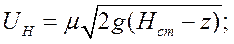
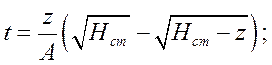
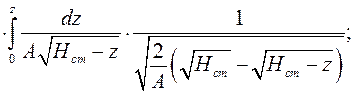
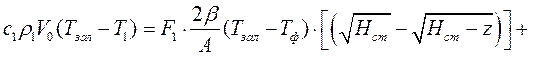
Расчет потери для наклонного канала в комбинированной форме.

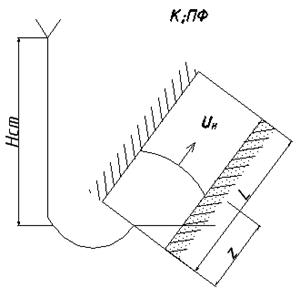
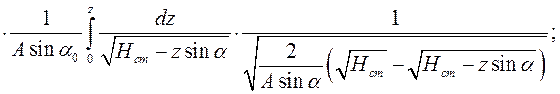
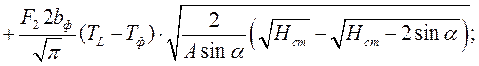
Потери в ПФ с песчаным стержнем.

Реальный случай

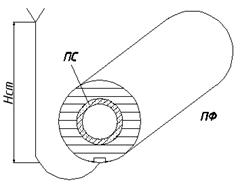
Разбивается на 4 канала.

В канале 2 и 3 учитывается суммарная площадь поперечного сечения.

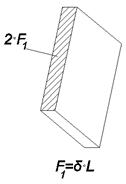
Анализ потерь перегрева при заполнении отливки в кокиле.

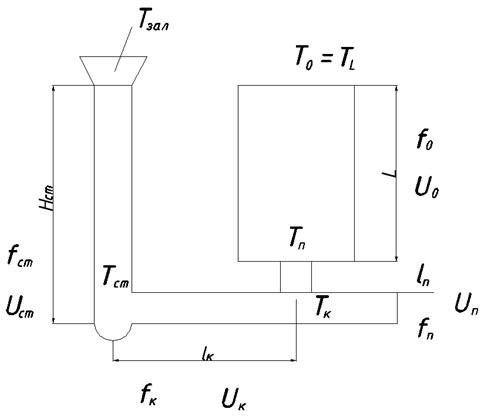
Для 1-го канала:

Для коллектора:

Для питателя:

Для отливки:

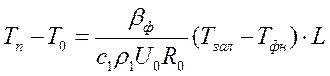или ()

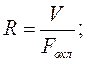
Т.к расход одинаковый, то:

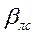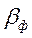Уменьшать и где .

- тепорпроводность краски;

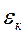- толщина краски;

При литье в металлический формы используют расширяющиеся литниковые системы.

Ø Длины каналов надо уменьшать;

Ø Использовать щелевые и ярусные питатели;

Ø Увеличивать ;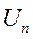

Ø Увеличивать приведенные размеры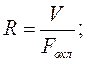

!!! Каналы надо стремиться делать цилиндрическими.

Возможный вариант - литье выжиманием:

Получение тонкостенных отливок.

Также желательно повышать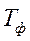

Использование центробежной заливки:

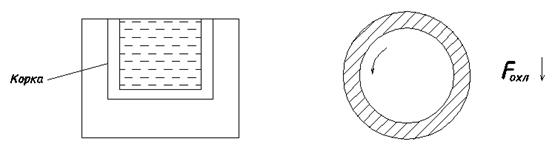
Способ выжиманием также снижает потери.

Анализ потерь перегрева при заполнении отливки в ПФ.

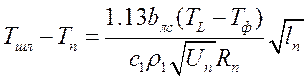
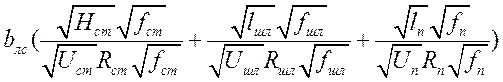
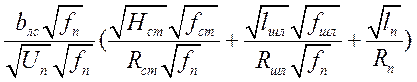
Ø Уменьшают , , , , , , .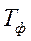

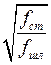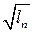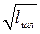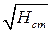Ø Желательно заливать в сухие песчаные формы.

Ø Используют в основном сужающиеся литниковые системы.

Ø Используют также разветвленную литниково-питающую систему.

Ø Увеличивают R засчет извлечения формы (сфера,цилиндр), а не засчет изменения массы.

Эвтектикосодержащий сплав.

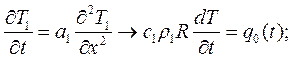
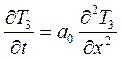
- для кокиля

- для ПФ

Затвердевание твердого раствора

(модель малой интенсивности охлаждения).

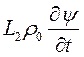- распределение тепловой кристаллизации.

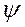- относительное кол-во твердой фазы от 0 до 1.

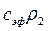- эффективная удельная теплоемкость.

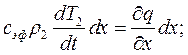
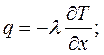
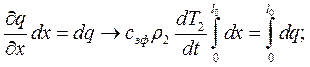
Это уравнение для двухфазной зоны модели малой интенсивности охлаждения.

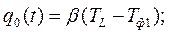- для кокиля;

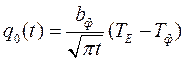- для ПФ;

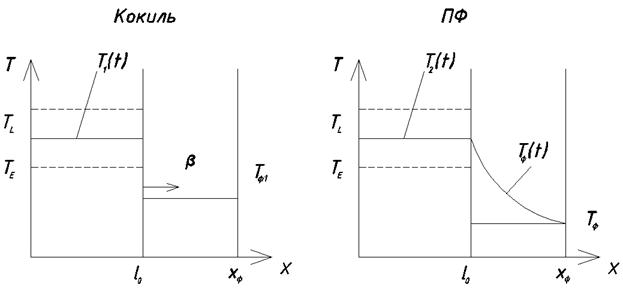
Расчет для кокиля:

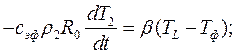
Н.У.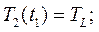

Н.У.

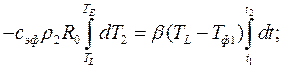
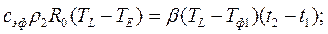
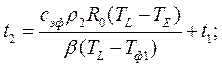- время затвердевания твердого раствора в кокиле.

Твердый раствор в ПФ:

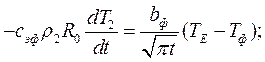
Время затвердевания эвтектики.

В модели малой интенсивности перепадом температур, но физически этот перепад существует как следствие последовательного затвердевания.

Кокиль

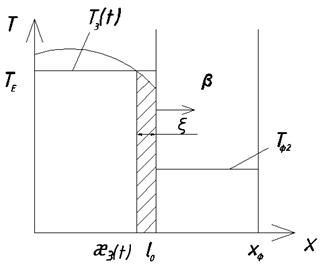
ПФ

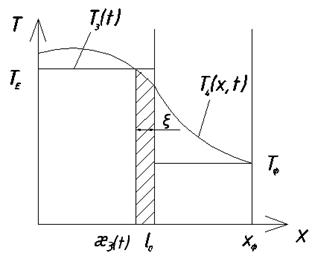
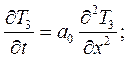
Г.у:

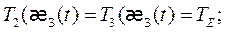
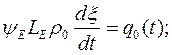
Время затвердевания эвтектики в кокиле.

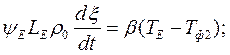
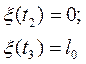
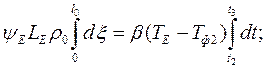
В общем случае заменяем на .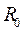

Время затвердевания эвтектики в ПФ.

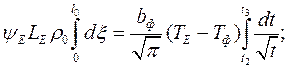
Расчет времени охлаждения отливки до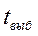

Н.У.

Н.У.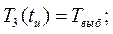

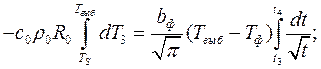
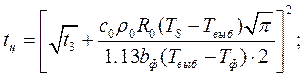
Н.У.

Н.У.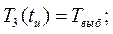

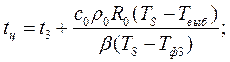
Пример расчета заполнения и затвердевания отливки.

ПФ

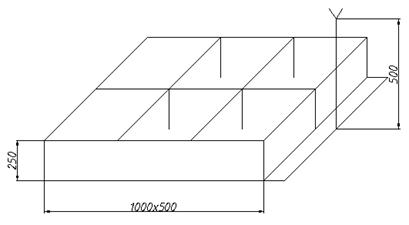
Равностенная отливка.

1. Время заполнения.

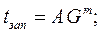, где G – масса отливки, A,m – коэффициенты.

A = 1,6…5,6 Принимаем: A = 3,8

m = 0,3…0,5 m = 0,4

G=420кг. Следовательно:

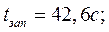
2. Определим площадь узкого места.

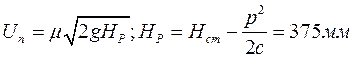
Сч 18 при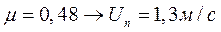

Сч 18 – эвтектический расплав.

,,

,,.

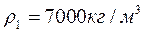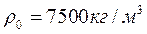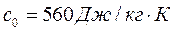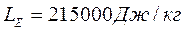- удельная теплота эвтектики.

, .

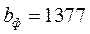Потерями перегрева в литниковой системе пренебрегаем.

2 канала: дно и заполнение вверх.

Заполнение горизонтального канала (дно).

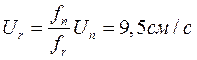
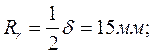
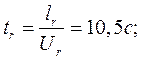
Потери при заполнении вертикального канала:

- площадь продольных каналов.

- площадь поперечных каналов.

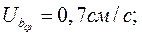
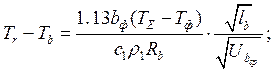
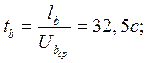
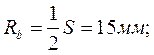
Выбираем max :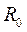

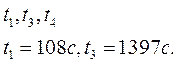
Для обычной стенки получилось бы: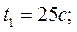

считается для среднего приведенного размера.

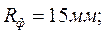
считается как будто форма и отливка – единое целое.

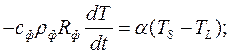(формы)

Песчаный наполнитель.

Влияние скорости затвердевания отливки на ее структуру.

Структурная диаграмма Клингенштейна.

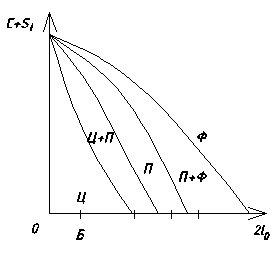
П – перлит;

Ц – отбел (белый чугун);

Ц – карбит Fe ()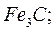

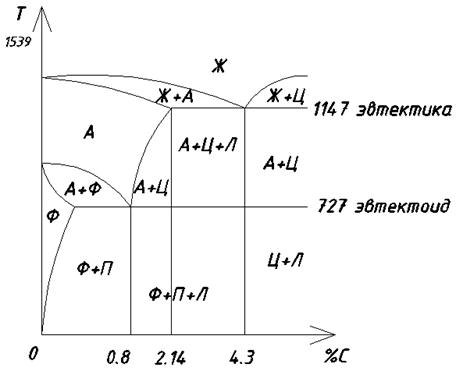
Метастабильная диаграмма затвердевания при малых скоростях затвердевания.

Структурная диаграмма Ершовича.

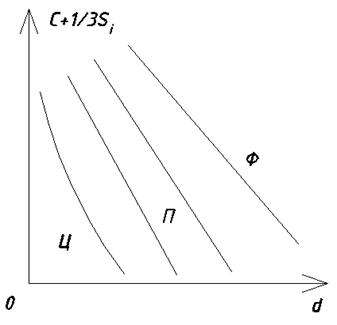
Когда считается углеродный эквивалент – то считается и 1/3 кремния ().

Структурная диаграмма Жукова.

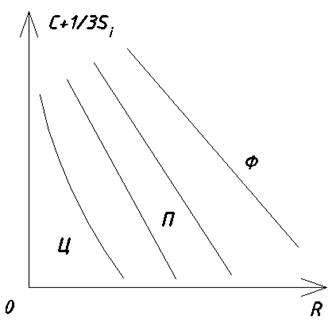
Структурная диаграмма Ланда.

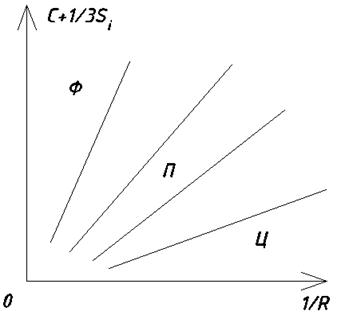
Структурная диаграмма для К_ф Дубинина.

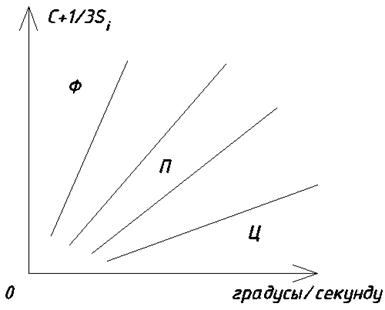
Во всех диаграммах дают существенное количественное расхождение.

Расчет скорости затвердевания отливок.

- скорость охлаждения;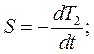

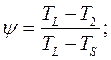
- отношение затвердевшей части ко всему объему отливки.

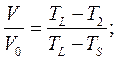
Продифференцируем это уравнение:

Делим обе части на

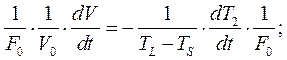
- эквивалентная скорость затвердевания отливки.

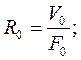
Получаем, что:

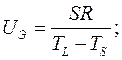
Структурная диаграмма Баландина.

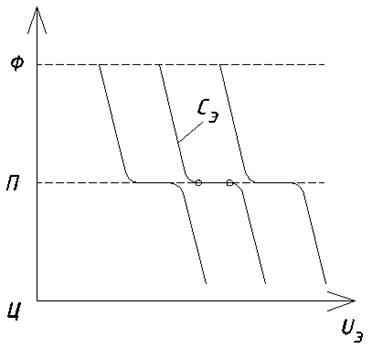
- углеродный эквивалент.

Главное отличие – наличие в интервале 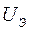. Получается одна и та же структура.

Дата добавления: 2014-01-07