Червячно-модульные фрезы

Зуборезные инструменты, работающие методом центроидного огибания

Червячно-модульные фрезы (ЧМФ) изготавливаются на основе червяка (основной червяк), который при своем вращении создает эффект бесконечно движущейся инструментальной рейки, что позволяет изготавливать ЗК с любым z, не прибегая к процессу деления, который может иметь место при нарезании ЗК зуборезной рейкой, когда ее длина меньше длинны начальной окружности нарезаемого колеса.

В машиностроении известны следующие три типа основных червяков:

1) эвольвентный червяк;

2) конвалютный червяк;

3) архимедов червяк.

Архимедов червяк получается как результат винтового движения прямой образующей линии, проходящей через ось винтового движения. Сечение этой винтовой поверхности плоскостью, перпендикулярной оси винтового движения, дает архимедову кривую.

Эвольвентная винтовая поверхность получается при обкатывании без скольжения образующей прямой линии по основному цилиндру, расположенному соосно оси винтового движения. При этом образующая линия является касательной к винтовой линии на основном цилиндре. В сечении эвольвентно-винтовой поверхности плоскостью, перпендикулярной оси винтового движения, получается эвольвента.

Конвалютная винтовая поверхность получается в результате винтового движения образующей прямой линии, параллельной прямой образующей при получении эвольвентной винтовой поверхности и отстоящей от нее на некотором расстоянии либо в «+», либо в «-». В сечении этой винтовой поверхности плоскостью, перпендикулярной оси винтового движения, получим конвалюту.

Рассмотрим линии, получаемые в различных сечениях этих трех червяков (рис. 2.1.1).

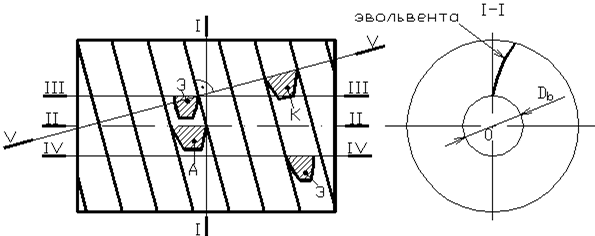
Рис. 2.1.1.

сечения	Вид кривой
Эвольвента	Конвалюта	Архимедова кривая
I-I	эвольвента	конвалюта	Архимедова спираль
II-II	кривая	кривая	прямая
III-III	лев.- прямая прав.- кривая	кривая	кривая
IV-IV	лев.- кривая прав.- прямая	кривая	кривая
V-V	кривая	прямая	кривая

Рис. 2.1.2. Профиль зуба ЧМФ на основе эвольвентного червяка в сечениях I-IV.

Теоретически самое точное ЗК может быть изготовлено ЧМФ на основе эвольвентного червяка (рис. 2.1.2). Однако эта точность будет обеспечена только до первой переточки зуба фрезы, т.к. при этой переточке не сохраняется требуемый профиль боковой поверхности зуба ЧМФ.

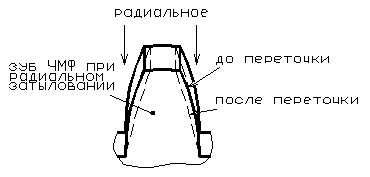
Рис. 2.1.3. Схема радиальной переточки зуба ЧМФ.

Сохранить точный профиль боковой поверхности зуба можно, применив осевое затылование (рис. 2.1.4).

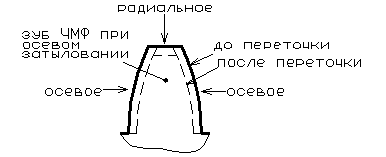
Рис. 2.1.4. Схема осевого затылования зуба ЧМФ.

Однако при этом зуб становится тоньше (т.е. возможна переточка только в пределах допуска на ширину впадины нарезаемых ЗК). Кроме того, нужно радиальное затылование для вершины зуба – трудоемкость увеличивается.

Все это привело к тому, что эвольвентный червяк на практике не используется для изготовления ЧМФ.

Использование архимедова червяка теоретически дает менее точные ЗК, но из-за того, что профиль зуба этого червяка в осевом сечении II-II прямолинеен, этот червяк может быть проконтролирован на точных измерительных средствах по углу профиля боковой поверхности зуба, осевому шагу и толщине зуба. Этот червяк наиболее часто применяется для изготовления чистовых ЧМФ.

Конвалютные червяки используются для изготовления неточных ЧМФ, для предварительной черновой обработки ЗК (например, дальнейшая обработка ЗК производится шевером или шлифованием после закалки).

Как указано выше для изготовления чистовых ЧМФ в основном применяются архимедовы червяки. Для изготовления стандартных ЗК профиль инструментальной стандартной рейки должен находиться в нормальном к виткам червяка сечении на его расчетном диаметре (см. ниже).

Определим угол профиля зуба архимедова червяка в осевом сечении по известному углу профиля ИР α = 20º и углу наклона винтовой линии на расчетном диаметре ω_t (рис. 2.1.5).

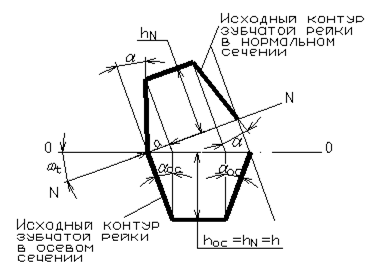
Рис. 2.1.5. Схема к определению угла профиля зуба архимедова червяка.

Задний угол в осевом сечении α_ОС необходим для контроля угла профиля ЧМФ в ее осевом сечении при угле наклона стружечных канавок ω_К = 0. Равенство расчетного и измеренного на каком либо приборе α_ОС доказывает точность изготовления фрезы по углу профиля.

ЧМФ также могут изготавливаться с ω_К ≠ 0, а именно ω_К = ω_t, т.е. стружечные канавки расположены перпендикулярно виткам червяка на его расчетном диаметре. В этом случае на виде на переднюю поверхность зуба ЧМФ при направлении взгляда перпендикулярно ее оси, мы увидим неодинаковые углы профиля на левых и правых боковых сторонах зуба фрезы (вершина зуба вверху). Это изменение углов происходит из-за радиально затылованной задней поверхности зуба ЧМФ (рис. 2.1.6).

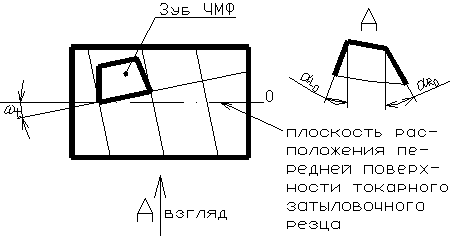
Рис. 2.1.6.

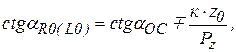
где к- величина падения затылка основного (первого) затылования ЧМФ;

z₀ – число стружечных канавок ЧМФ;

Р_z – осевой шаг винтовых стружечных канавок ЧМФ.

Поскольку в осевом сечении архимедова червяка боковые поверхности зуба являются прямыми линиями, то эти параметры (α_ОС, α_L0, α_R0) легко и точно контролируются (могут быть изготовлены точными ЧМФ – получить точные ЗК).

В зависимости от степени точности нарезаемого ЗК ЧМФ могут быть изготовлены с разной степенью точности, которая обозначается буквами АА, А, В, С, Д (слева направо точность убывает).

Например: ЧМФ класса точности АА (прецизионные ЧМФ) позволяют изготовить ЗК 7-ой степени точности.

Дата добавления: 2014-01-07