Аналитическая модель процесса теплопроводности

В общем виде нестационарный процесс нагрева в линейной постановке для бесконечного цилиндра описывается уравнением в частных производных

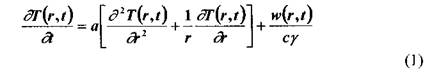
с граничными условиями, например 2-го рода

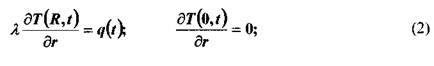
и начальными условиями

Здесь - коэффициент удельной теплопроводности; 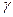- удельная плотность материала; а - коэффициент температуропроводности, 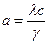, с - коэффициент удельной теплоемкости, w - функция источников тепла, q - плотность потока тепловых потерь.

Распределение источников тепла обычно задается в виде простой функции для удобства последующего интегрирования, хотя принципиальных ограничений на вид этой функции нет.

С помощью метода интегральных преобразований возможно аналитическое решение системы, то есть получение явного выражения для состояния в любой точке в любой момент времени.

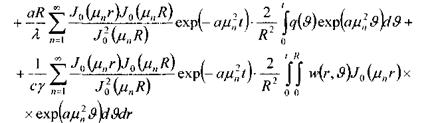
где

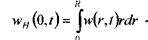изображение функции источников,

полученное с помощью преобразования Ханкеля.

В представленном решении собственные числа 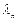определяются из характеристического уравнения, составляемого на основании граничных условий подстановкой в них собственных функций

Проанализируем выражение для определения температуры. В решении содержатся компоненты, соответствующие внутренним источникам тепла, тепловым потерям и начальному состоянию. В первой строке выражения (4) записаны компоненты, формирующие среднее значение температуры по всему объему нагреваемого тела. В последующих строках записаны уточняющие выражения, обеспечивающие создание кривой распределения температуры по координате (r), отражая вклады начального распределения температуры f(r), тепловых потоков q(t) и мощности w(r,t).

Постановка задачи подразумевает, что указанные компоненты заранее обусловлены, то есть, выражены в виде определенных функций как во времени, так и в пространстве. Это приводит к тому, что временная зависимость температуры каждой точки может быть построена путем расчета для нескольких конечных моментов времени из неизменных начальных условий при неизменных значениях потоков тепла и мощности источников.

Более сложная ситуация, возникающая при использовании такой модели при разработке программного (многоинтервального) управления требует более громоздкого алгоритма.

Использование выражения (4) требует на каждом интервале пересчета начального распределения температуры, задания нового значения мощности (максимум или ноль), пересчета тепловых потоков (не всегда).

1. Для аппроксимации переходной характеристики используется программа Matlab, которая позволяет решить поставленную задачу наиболее простым путем и обладающая набором специальных функций по данной тематике.

Одним из возможных решений служит применение зависимости температуры от времени для неограниченного цилиндра:

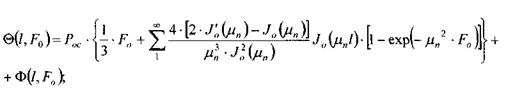
с начальными условиями: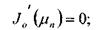

где F_o, Р_ос -критерии Фурье и Померанцева соответственно; J₀ -функция Бесселя; 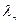-корни полученные при решении (2); l -координата контрольной точки;

Передаточная функция переходного процесса будет равна отношению изображения температуры к изображению входного сигнала, в данном случае в качестве входного сигнала выступает единичная функция Хевисайда.

В результате получиться передаточная функция вида:

Получение упрощенной передаточной функции происходит методом подбора коэффициентов стандартных звеньев и их комбинация. Преимуществом данного способа является его универсальность, так как зависимость (1) уже подразумевает наличие решения дифференциального уравнения второго порядка. Среди недостатков можно выделить достаточную трудоемкость. 2. Следующим методом аппроксимации служит метод наименьших квадратов, который базируется на принципе минимума квадрата разности между значениями аппроксимирующей и аппроксимируемой функций.

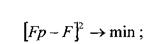
где F -исходная переходная характеристика;

Поиск экстремума данной разности квадратов связан с необходимостью правильного выбора модели, в нашем случае аппроксимирующая модель будет иметь вид:

В программе Matlab существует процедура expfit (x,y,z), которая производит поиск регрессионную зависимость в виде:

Где: х - матрица значений аргумента переходной функции;

y - матрица значений переходной функции;

z - матрица (З х l) которая несет информацию о знаках

при коэффициентах а,b,с;

Полученный результат в виде матрицы (3 х l) соответствует значениям коэффициентам а,b,с;

Преимущество этого метода заключается в возможности аппроксимации практически любых переходных характеристик. В случае если полученная модель не адекватна (большая ошибка приближения) следует выбрать более сложную модель. В данном случае аппроксимация производится двумя экспонентами

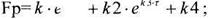
Для определения коэффициентов k_п записывается система n -

уравнений и с помощью стандартных операторов происходит ее решение. Для решения используются точки исходной переходной характеристики. Правильность выбора точек показывает значение ошибки приближения.

Аппроксимация других переходных характеристик производится с помощью процедур заложенных в программу.

Дата добавления: 2014-01-07