Расчет поля диполя

Диполь – система двух точечных разноименных по знаку, равных по величине зарядов (q), расположенных очень близко друг к другу. Эта система имеет большое значение при рассмотрении ряда вопросов. Любой атом – это диполь, именно свойствами атомов объясняются электрические, магнитные и др. свойства твердых тел.

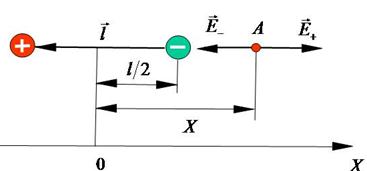Изобразим диполь и рассчитаем его поле в точке А, которая лежит на продолжении плеча диполя (Рис.5).

где 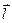- плечо диполя; 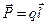- дипольный момент

- Электрическое поле в точке А складывается из полей заряда q+ и q-. Согласно принципа суперпозиции имеем:

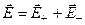в проекции на ось Х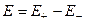

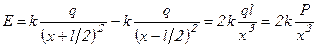
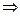
- Пользуясь законом Кулона рассчитываем напряженность поля в точке А 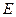~ 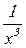(8.14)

- Определим потенциал поля в выбранной точке

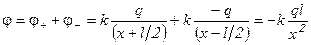
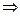
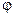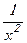~ (8.15)

Теперь рассчитаем поле диполя в точке, которая лежит на перпендикуляре, проведенном через середину плеча диполя, в точке В (Рис.6).

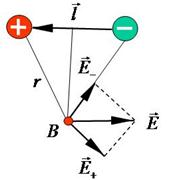
Из подобия треугольников и, учитывая, что 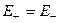, рассчитаем напряженность в точке В:

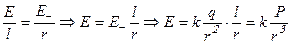
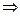
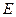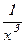~ (8.16)

Потенциал поля в этой точке равен алгебраической сумме потенциалов:

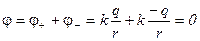. (8.17)

Подведем итог сказанного, сравнивая результаты расчета полей точечного заряда и системы двух точечных зарядов - диполя:

- напряженность поля точечного заряда обратно пропорциональна квадрату расстояния до выбранной точки 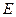~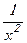; напряженность поля диполя (системы двух точечных зарядов) обратно пропорциональна расстоянию в третьей степени ~.

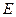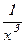- потенциал поля точечного заряда обратно пропорционален расстоянию до выбранной точки 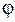~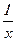; потенциал поля диполя (системы двух точечных зарядов) обратно пропорционален квадрату расстояния ~.

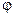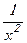Теперь следует перейти к расчету полей распределенных зарядов – по нити, поверхности, объему. В этом случае необходимо распределенный заряд разделить на точечные заряды. Для каждого точечного заряда определить напряженность поля в заданной точке. Затем, воспользовавшись принципом суперпозиции, сложить все поля точечных зарядов. Количество слагаемых бесконечно велико и задача становится очень громоздкой. Существует ряд приемов решения этой задачи. Например, теорема Гаусса.

Рассмотрим поведение диполя в однородном электрическом поле (Рис.7).

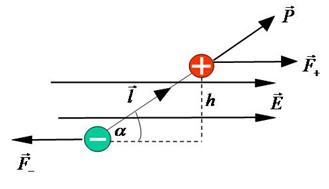
Действует пара сил, которая создает вращающий момент:

.

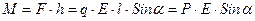В векторном виде имеем:

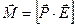. (8.18)

Результирующая сила, действующая на диполь в однородном электрическом поле, равна нулю. Диполь как целое не будет перемещаться в пространстве, но возникает момент пары сил, который ориентирует диполь. Поле устанавливает диполь таким образом, чтобы дипольный момент 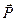был направлен вдоль вектора напряженности поля .

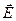Найдем работу внешних сил по повороту диполя на угол α:

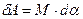. Эта работа пойдет на увеличение потенциальной энергии диполя:

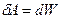
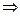
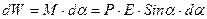После интегрирования получаем:

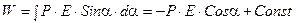. (8.19)

Будем считать, что при α=90⁰ потенциальная энергия диполя равна нулю:

.

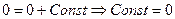Окончательно значение для потенциальной энергии принимает вид:

(8.20)

Проанализируем полученное уравнение:

- Пусть α=00 тогда 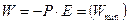. Это положение устойчивого равновесия.

- Пусть α=900 тогда .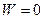

- Пусть α=1800 тогда 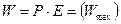. Это положение неустойчивого равновесия.

Если диполь находится в неоднородном поле, то он будет перемещаться в пространстве под действием силы, которую определим по уравнению:

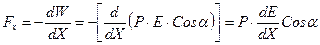. (8.21) Будем считать, что 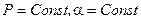, 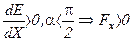. Это значит, что диполь будет втягиваться в область более сильного поля.

Будем считать, что 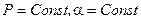, 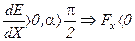. Это значит, что диполь будет выталкиваться из области более сильного поля в область более слабого.

Дата добавления: 2014-01-07